Friction on Mesoscopic Scale

Elastic slider  

In what follows we discuss collective effects in the frictional interface trying to clarify, in particular, the following questions: (i) what is the law of interaction between the contacts; (ii) at which scale can the slider be considered as a rigid body, or what is the coherence distance λ_c within which the motion of contacts is strongly correlated; (iii) whether the interaction effects can be incorporated in the master equation approach; (iv) how does the interaction between the contacts modifies the interface dynamics; (v) what is the screening length λ_s; (vi) when do avalanche motion of contacts (a self-healing crack) appear, what is the avalanche velocity and (vii) the propagation length Λ?

Elastic constant of the slider. The slider (shear) elastic constant K is equal to K = [E/2(1+ν)](L_xL_y/H), where L_x, L_y and H are the slider dimensions, E and ν are the substrate Young modulus and Poisson ratio, respectively. For example, for a steel slider of Young's modulus E=2×10¹¹ N/m², Poisson's ratio ν=0.3 and the size L_x×L_y×H = 1 cm × 1 cm × 1 cm, we obtain K ~ 10⁹ N/m.

Rigidity of the interface contacts. Next, let us characterize the typical magnitudes of the contact stretching length x_c and stiffness k_c. Assume the slider and the substrate to be coupled by N = L_xL_y/a² contacts, and that the contacts have a cylindrical shape of (average) radius r_c with a distance a between the contacts. It is useful to introduce two dimensionless parameter. The first parameter γ₂= r_c/a  characterizes the density of contacts and may be estimated as follows. Consider a cube of linear size L on a table. The weight of the cube F_l= ρL³g  (ρ is the mass density and g=9.8 m/s²) must be compensated by forces from the contacts, F_l= Nr_c²σ_c, where σ_c is the plastic yield stress. Then, γ₂²= (Nr_c²)/(Na²) = (ρL³g)/(σ_cL²), or γ₂= (ρLg/σ_c )^1/2. Taking L = 1 cm, ρ = 10 g/cm³ and σ_c= 10⁹ N/m² (steel), we obtain γ₂≈ 10^–3 which should be typical for a contact of rough stiff surfaces. For softer materials, and especially for a lubricated interface, the values of γ₂ would be much larger, e.g., γ₂~ 0.1.

The second dimensionless parameter γ₁= k_c/Ea characterizes the stiffness of the contacts. To estimate γ₁, assume that contacts have the shape of a cylinder of radius r_c and length h (h is the thickness of the interface). Suppose in addition that one end of a contact ("column") is fixed, and a shear force  f  is applied to the free end. This force will lead to the displacement x = f /k_c of the end, where k_c= 3E_cI/h³,  E_c is the Young modulus of the contact material and I = πr_c⁴/4 is the moment of inertia of the cylinder. In this way we obtain k_c= (3π/4)(E_cr_c)(r_c/h)³, so that γ₁= (3π/4)(E_ca³/Eh³)(r_c/a)⁴= γ₀γ₂⁴  with γ₀= (3π/4)(E_c/E)(a/h)³. For the contact of rough surfaces, where E_c= E and a > h, we have γ₀ > 1, while for lubricated interfaces where E_c<< E, one would expect γ₀ < 1.

An estimate of characteristic values leads to r_c~ (10^–3−10^–2) a.  Thus, for the steel slider considered above, taking r_c= h = 1 μm and intercontact spacing a = 3×10²r_c, we obtain N ~ 10³ and k_c~ 5×10⁵ N/m, so that the global stiffness of the interface is K_s~ 5×10⁸ N/m.

Interaction between contacts

First let us consider the question how the forces on contacts are redistributed when one of contacts breaks. A qualitative picture of elastic interaction is presented in Fig.I1 (left). When a contact acts on the surface at r=0 with a force f, it produces a displacement field u(r) ∝ r^–1 which affects other contacts (Fig.I1a) − similar to the Coulomb potential for a point charge. However, if there are two surfaces, then the same contact acts on the second surface with the opposite force −f  and, if the two surfaces are in contact, the resulting displacement field should fall as u(r) ∝ r^–3 (Fig.I1b) − similar to the dipole-dipole potential for a screened point charge near a metal surface. The question thus is the form of the interaction for the multi-contact interface (Fig.I1c).

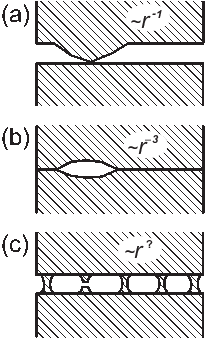Figure I1:   Left: decaying of the displacement field at the interface (schematic): (a) for a single contact u(r) ∝ r–1, (b) for a single hole u(r) ∝ r–3, (c) for the array of contacts.   Right: change of forces on contacts when the central contact is removed (γ1= 0.06).

In what follows we show that the interaction between the contacts demonstrates a crossover from the r^–1 slow Coulomb decay at short distances to the faster dipole-dipole one at large distances.

Analytics. Let us consider an array of N elastic contacts with coordinates r_i={x_i, y_i, 0}, i=1,...,N  between the two (top and bottom) substrates. If the interface is in a stressed state, the contacts act on the top substrate with forces f_i={f_ix, f_iy, f_iz}. These forces produce displacements u_i^(top) of the (bottom) surface of the top substrate. The 3N-dimensional vectors U^(top)={u_i^(top)}  and  F_t={f_i} are coupled by the linear relationship U^(top) = G^(top)F_t. The elements of the elastic matrix G^(top) (known also as the elastic Green tensor) for a semi-infinite isotropic substrate are given in the Landau and Lifshitz texbook:

In the equilibrium state, the forces that act from the contacts on the bottom substrate, must be equal to F_b = −F_t according to third Newton's law. These forces lead to displacements of the (top) surface of the bottom substrate, U^(bottom)= −G^(bottom)F_t. The elements of the bottom Green tensor G^(bottom) are defined by the same expressions (I9) except the xz elements for which G_{ix, jz}^(bottom)= −G_{ix, jz}^(top)  (if the substrates are identical, the z displacements are irrelevant). Thus, the relative displacements at the interface due to elastic interaction between the contacts are determined by

U = U(top) − U(bottom) = − GF ,

(I10)

where F = −F_t and G = G^(top) + G^(bottom).

On the other hand, the forces and displacements are coupled by the diagonal matrix (the contacts' elastic matrix) K with elements K_iα, jβ= k_iαδ_ijδ_αβ  (α,β = x,y,z):

F = K ( U0 + U ) ,

(I11)

where U₀ defines a given stressed state (because of linearity of the elastic response, final results should not depend of U₀). The total force at the interface, f = Σ_if_i, must be compensated by external forces applied to the substrates, e.g., by the force f^(ext)= f applied to the top surface of the top substrate if the bottom surface of the bottom substrate is fixed.

Combining Eqs.(I10) and (I11), we obtain F = K ( U₀− GF ), or

F = BKU0 ,   where   B = ( 1 + KG )-1.

(I12)

If now one changes the contacts' elastic matrix, K → K + δK, then the interface forces should change as well, F → F + δF. From Eq.(I12) we have δF = (δB)KU₀+ B(δK)U₀. Then, δB may be found from the equation δ[B(1+KG)] = (δB)(1+KG) + B(δK)G = 0 . Therefore, finally we obtain:

δF = B δK (1 − GBK) U0 .

(I13)

Above we have assumed that δK is small. If it is not so, one has to use the expression δF = B δK (1 − GBK) U₀ with K = (1 + δK GB)^-1(K + δK).

Now, if we remove the i^*th contact by putting δk_iα= −k_iαδ_ii^*  and then calculate the resulting change of forces on other contacts, we can find a response of the interface to the breaking of a single contact as a function of the distance  r = r_i− r_i^*  from the broken contact.

Numerics. Equation (I13) may be solved numerically by standard methods of matrix algebra. We explore an array of identical contacts, k_iα= k_c and (U₀)_iα= u₀δ_αx for all i, organized in a square 89×89 lattice with spacing a=1, with the broken contact i^* at the center of the lattice. For singular terms of the Green function (9) we apply a cutoff at r_ii= r_c. Numerical results depend on two dimensionless parameters. The first one, γ₁= k_c/E_*a, determines the stiffness of the array of contacts relative the substrates (here E_*^–1 = E_top^–1 + E_bottom^–1). The second parameter γ₂= r_c/a  characterizes the density of asperities. A typical distribution of force changes induced by breaking of the central contact is shown in Fig.I1 (right).

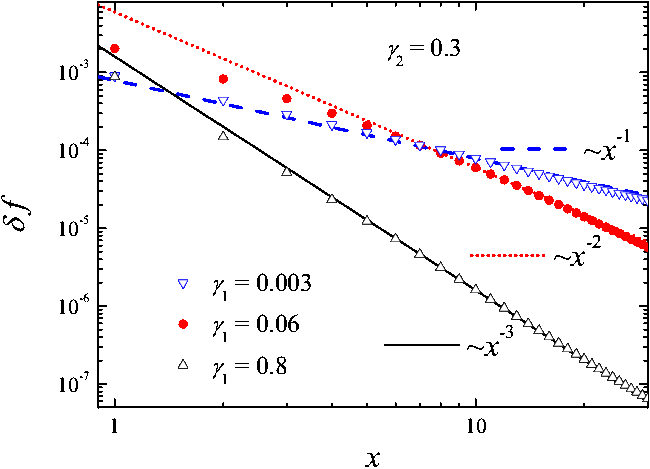Figure I2: Dependence of the change of forces δf(r) on the distance x from the broken contact. Left: δf(r) for three values of the interface stiffness: γ1= 0.003 (blue down triangles, dashed line), 0.06 (red solid circles, dotted line) and 0.8 (black up triangles, solid line) at fixed value of γ2=0.3 (ν=0.3). The lines show the corresponding power laws. Right: schematic picture.

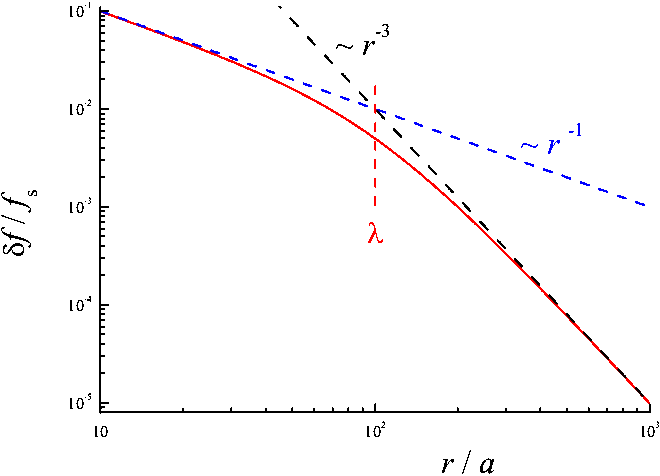
The numerical results for the x-component of dimensionless force δf = δF_x/(k_cu₀) are presented in Fig.I2. The function δf(r) exhibits a crossover from a slow Coulomb-like decay δf(r) ∝ r^–1 at short distances r << λ_c to the fast dipole-dipole-like decay δf(r) ∝ r^–3 at large distances r >> λ_c. The near and far zones are separates by the elastic correlation length λ_c first introduced by Caroli and Nozieres (1998). It may be estimated in the following way: the stiffness of the "rigid block" K ~ Eλ_c should be compensated by that of the interface, K ~ k_c(λ_c/a)² (stiffness of one contact times the number of contacts). This leads to

The rigid slider corresponds to the limit E → ∞, or γ₁→ 0. Therefore, the slider may be considered as a rigid body (e.g., in MD simulation), if its size is smaller than λ_c. For example, for a steel slider estimation gives λ_c/a ~10². Up to distance λ_c the contacts strongly interact. If the ith contact breaks and its stretching changes on |δx_i| ≈ x_c, then the force on the jth contact at a distance r_ij < λ_c away, changes by δf_j ≈ κk_ca δx_i/r_ij , where the dimensionless parameter κ < 1 characterizes the strength of interaction (numerics gives κ ~10^–3). In the near zone r << λ_c the interaction between the contacts may be accounted for within the master equation approach in a mean-field fashion as described in next section. At larger distances, different regions of the slider will undergo different displacements. Therefore, in the far zone, r >> λ_c, we must take into account the elastic deformation of the slider.

Nearby contacts: MF approach

Let us now include the dynamical interaction between the contacts. When a contact breaks, the now unsustained shear stress must be redistributed among the neighboring contacts. Using the results of previous section, we assume that because of elastic interaction between the contacts i and j, the forces acting on these contacts have to be corrected as  f_i→ f_i− Δf_ij  and  f_j→ f_j + Δf_ij, where Δf_ij = k_ij(x_j− x_i) in linear approximation. For example, let at the beginning the contacts be relaxed, x_j(0) = x_i(0) = 0. Due to sliding motion, all stretchings grow together, so that still Δf_ij= 0. At some instant t let the jth contact break, x_j(t) → 0, while the ith contact is still stretched, x_i(t) > 0. Clearly, as the jth contact breaks, the force on the ith contact increases, Δf_ij(t) = −k_ijx_i(t) < 0. The amplitude of interaction decreases with the distance r from the broken contact as Δf ∝ r^–1 at short distances r < λ_c. Neglecting the anisotropy of interaction, we assume that k_ij= f /|r_ij|, where  f  is a parameter.

Figures I3 and I4 show the result of simulations for different values of the dimensionless strength of the interaction

κ = f /(kcxc) ,

(I15)

where x_c= ∫dx xP_c0(x) is the average stretching of the initial threshold distribution (for the rectangular distribution x_c= x_s). These results yield the following conclusions. First, in the steady state, the interaction causes a narrowing of the final distribution Q_s(x). At high interaction strength κ, the distribution approaches a narrow Gaussian one. Second, the drop of frictional force F(X) at the onset of sliding (at X ~ x_c) gets steeper and steeper as κ grows. Therefore, contact interactions reinforce elastic instability. Third, above a critical interaction strength, κ ≥ κ_c~ 0.1, a multiplicity of contacts break simultaneously at the onset of sliding, and there is an avalanche, where the force F(X) drops abruptly.

Figure I3: The steady state distribution Qs(x) for the rectangular threshold distribution Pc0(x) with xs= 1 and Δxs= 0.25 and different values of the interaction strength κ = 0, 0.02, 0.06, 0.1, and 0.5.   The EQ simulations (dotted) are compared with the ME results (solid blue curves).

Figure I4: Onset of sliding: the initial part of the dependence of the friction force F on the slider displacement X for different strength of interaction κ = 0.005 (black), 0.01 (cyan), 0.03 (red), 0.05 (blue), and 0.07 (magenta).   Dotted curves show the results of EQ simulation, and solid curves, the mean-field ME approach.   The threshold distribution Pc0(x) has the rectangular shape with xs= 1 and Δxs= 0.25.

While the EQ model may be studied numerically only, it would be useful to have some analytical results. In what follows we show that the EQ results may be reproduced within the ME approach by using "effective" P_c(x) and R(x) distributions defined in a mean-field fashion. 

Smooth sliding. Using the steady state solution of the ME, one may approximately recover the functions P_c(x) and R(x) if the stationary distribution Q_s(x) is known. Indeed, for small x, where P(x) is close to zero, the left-hand side of Q_s(x) allows us to find R(x) as R(x) ∝ Q_s'(x), while the right-hand side of Q_s(x), where x~x_c and the contribution of R(x) to the shape of the steady state distribution is negligible, gives us P_c (x) ∝ P(x)Q_s(x) ∝ −Q_s'(x). (e.g., see Fig.2 in the ME-Introduction). Thus, differentiating the function Q_s(x) obtained in the EQ simulation, we may guess shapes of the effective distributions P_c(x) and R(x) which, when substituted in the ME, would produce a solution Q_s(x) close to that obtained in the EQ simulation.

Using the simulation results, let us suppose that the detached contacts form again with nonzero stretchings, i.e., that the distribution R(x) is shifted to positive stretching values,

R(x) = G( x − αxc, γxc ) ,

(I16)

where G(x,σ) is the Gaussian distribution with zero mean and standard deviation σ. At the same time, we suppose that the effective threshold distribution P_c(x) shrinks and shifts with respect to the original ("non-interacting") one,

Ph (x) = βPc0[β(x − αxc)] .

(I18)

Let us moreover take its convolution with the Gaussian function, P_c(x) = P_h⊗G = ∫dξ P_h(x − ξ) G(ξ, γ√2x_c).

The results of this procedure for the rectangular distribution P_c0(x) are shown in Fig.I3. We see that with a proper choice of the parameters α, β and γ, the ME solutions Q_s(x) perfectly fit the numerical EQ results (for the parameters α, β and γ in Fig.I3 we used expressions β = 1 + b₁κ, α = b₂κ/β and γ = b₃α − b₄α² with the coefficients b₁= 18, b₂= 9.6, b₃= 0.142 and b₄= 0.232). Results of similar quality were also obtained for other simulated cases, e.g., for larger radius of the interaction or for wider threshold distribution P_c0(x).

The dependences of the fitting parameters α, β and γ on the dimensionless strength of interaction κ may be found in the following way. Clearly that for noninteracting contacts we have α = γ = 0 and β = 1. It is reasonable to expect that in the lowest approximation α,γ ∝ κ and β−1 ∝ κ. Indeed, the shift of the effective distribution P_c(x) appears because of the interaction, αf_c= Σ_jΔf_ij , therefore at small κ we have approximately

α ~ 0.5a-2 ⌠ ⌡ λc 0  d2r κxc/|r| = πκλcxc/a2.

(I19)

At large κ, however, α has to saturate, e.g., as α ∝ κ/β, because the shift cannot be larger than x_c, i.e., α < 1. Then, because the distribution P_c(x) shrinks from both sides, we have b₁~ 2b₂.

Thus, the interaction makes the threshold distribution P_c(x) narrower by a factor β and shifts its center to the left-hand side, x_c→ νx_c, where ν = α + β^–1 changes from 1 to 0.5 as the interaction strength κ increases from zero to infinity.

Onset of sliding. The beginning of motion when started from the relaxed configuration, Q(x; 0) = δ(x), cannot be explained by the approach used above, because the effective distribution P_c(x) is "self-generated" during smooth sliding, when the process of contacts breaking-reattachment is continuously operating. Nevertheless, the initial part of the F(X) dependence may still be described by the effective ME approach, but with the modified "forward" threshold distribution given by the expression

Numerics shows that with a proper choice of the fitting parameters β₀ and ε₀ for a given value of κ, the initial part of the function F(X) may be reproduced with quite high accuracy. Moreover, for a rather wide range of κ values, the EQ simulation results may be reproduced by the ME approach with a reasonable accuracy using only three fitting parameter c₁, c₂ and κ_c, if the parameters β₀ and ε₀ in Eq.(I20) are given by the expressions β₀= 1 + c₁κ/(1 − κ/κ_c) and ε₀ =c₂(β₀- 1), where the parameter κ_c corresponds to the critical interaction strength when many contacts begin to break simultaneously. For κ > κ_c, the drop of F(X) becomes jump-like, so that K^*= ∞ and stick-slip will appear for any stiffness of the slider K < ∞; the value of κ_c may be estimated from the equation αx_c~ Δx_s.

For the rectangular shape of the distribution P_c0(x) the result of this procedure is demonstrated in Fig.I4 (the fitting parameters are c₁= 33.9, c₂= 3.0 and κ_c= 0.074).

Of course, the P_ci(x) function, Eq.(20), can describe only the initial part of the F(X) dependence, when F(X) grows, reaches the first maximum and then decreases. To simulate the whole dependence F(X), one would have to involve the evolution of P_c(x) with sliding distance, e.g., as some "aging" process P_ci(x) → P_c(x) (see ) with the initial distribution P_{c, ini}(x) = P_ci(x) and the final one P_{c, fin}(x) = P_c(x).

Stick-slip vs smooth sliding. As mentioned above, stick-slip appears as a result of elastic instability which is controlled by the relation between the slider stiffness K and the effective interface stiffness K^*. For noninteracting contacts K^*≈ K_sx_c/Δx_s; because typically Δx_s~ x_c, estimates give K^*< K so that stick-slip would never appear. The interaction between contacts strongly enhances the elastic instability thus making stick-slip much more probable. Indeed, because of the effective shrinking of the threshold distribution, the parameter K^* increases roughly as K^*→ K_eff^*~ β₀K^*, i.e., the effective interface stiffness K_eff^* grows with the strength of interaction κ, and the elastic instability can now emerge. For example, for a realistic threshold distribution the dependence of K_eff^* on the strength of interaction κ is shown in Fig.I5.

The strength of interaction between the contacts may be found as κ ≈ κa/x_c, where realistic values of the dimensionless parameter κ are of the order κ ~ 10^–3; taking  a ~ (10²−10³) r_c  and  x_c~ r_c, we obtain κ ~ 0.1−1 which gives β₀ ~ 3 − 13 according to Fig.I5.

Macrocontacts (λ-contacts)

Thus, within the area λ_c² the substrate can be considered as rigid. This allows us to split the friction problem in two parts. At the smaller scale one can study the collective behavior of a set of contacts attached to a "rigid body" of size λ_c, which is itself related to the bulk by an elastic spring of rigidity k_λ describing the elastic response of the part of material which is between the asperities and the bulk. We henceforth call λ-contact this set of microscopic contacts. The parameters of the λ-contact, such as its breaking threshold, or the effective elastic constant (the relation between its stretching and the shear stress applied between the bulk and the underlying substrate) may be calculated with the help of the ME approach, incorporating the interaction between the microcontacts within the MF approximation as described above. The strong inter-contact interaction leads to a narrowing of the effective threshold distribution for contact breaking and enhances the chances for an elastic instability to appear.

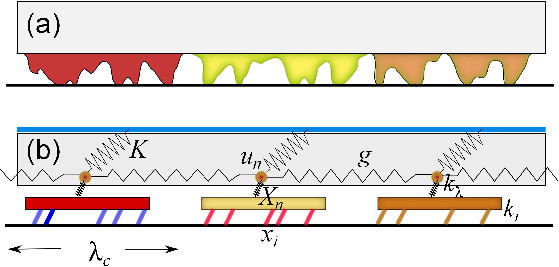Figure I6: Schematic view explaining the decomposition of the friction problem into elements that are studied separately. (a) Contact of a rough interface with a flat substrate. We consider the bulk material (rectangle) and the interfacial rough layer, which has many asperities in contact with the substrate. (b) The reduced model. Asperities are correlated over a length λc and form a "λ-contact" composed of asperities, having elastic constants ki, and a piece of material, between the asperities and the bottom of the bulk volume, having an elasticity kλ. The nth λ-contact is attached to the bulk material at position un. The bulk material is described by an elastic constant g that corresponds to its deformation along the interface, and the elastic constant K which is associated to its shear deformation when its top surface is subjected to some shear stress.

At a larger (mesoscopic) scale the elastic deformation of the sliding block cannot be ignored. The λ-contacts are elastically coupled through the deformation of the bulk. On distances above the correlation length, r > λ_c, the interaction between the λ-contacts leads either to screening of local perturbations in the interface, or to appearance of collective modes − frictional cracks propagating as solitary waves. Thus, to develop a full theory of friction on the mesoscale, one has to take into account the elastic deformation of the sliding blocks and the interface by introducing a position dependent distribution Q[x, X(r)], where r = {x,y} denotes the position of the λ-contact on the interface, and X(r,t) describes the local translation of the interface averaged over the λ_c scale. The solution of the master equation (or a set of equations if the aging is included) then provides a local force (stress) at the interface F(r,t). The master equation has then to be coupled to an equation describing the elastic deformation of the block with the boundary condition at the interface, subjected to the contact forces F(r,t) at each point r.  Such a program is realized in next section.

Next: Collective effects at frictional interface

Back to main page or tribology page

Last updated on May 3, 2014 by O.Braun.  Copyright © by O.Braun.  Translated from L^AT_EX by T_TH