Above we described the rigid motion of the top substrate, when the ME solution always leads to smooth sliding. In order to describe a real dynamics of a tribosystem, we have to take into account the following three issues: (i) the slider inertia, (ii) the elastic instability, and (iii) the delay in contact formation or/and their aging.
 First,
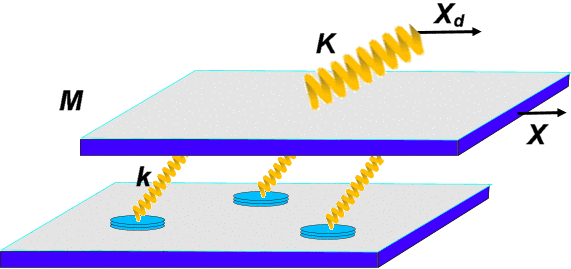
we have to involve the motion equation for the slider; let it be modeled as a rigid entity
(a nonrigid slider will be considered below) of mass M (see figure
First,
we have to involve the motion equation for the slider; let it be modeled as a rigid entity
(a nonrigid slider will be considered below) of mass M (see figure
![]() ).
The slider is driven through a spring of the elastic constant K with the velocity vd , so that the
(experimentally measured) spring force is Fd= K (Xd−X), Xd= vdt.
Also the slider experiences the force −F
from all contacts as described above with the ME or EQ approach. Every contact
at the interface moves
rigidly with the slider so long as the total force fi< fsi ,
where fsi is a threshold value. Above the
threshold the contact detaches from the slider and slips relative to it for a
delay time τd after which it stops and
attaches again to the slider; at this moment its stretching is determined from the condition that
the total force fi on the contact is equal
to the "backward" force fb~ 0. The force F from the interface
acting on the slider is the sum of the forces from the pinned contacts, fi(sub)= kixi (recall that xi is the stretchings of the
contact and ki is its elastic constant), plus additionally the sum of drag forces from the detached/sliding
contacts, fi(drag)
= −miηi [v−dxi(t)/dt
], where v(t) = dX(t)/dt is the
slider velocity, mi is the mass of the
contact and ηi is the
corresponding damping coefficient (e.g., the "viscosity" of the molten
lubricant).
).
The slider is driven through a spring of the elastic constant K with the velocity vd , so that the
(experimentally measured) spring force is Fd= K (Xd−X), Xd= vdt.
Also the slider experiences the force −F
from all contacts as described above with the ME or EQ approach. Every contact
at the interface moves
rigidly with the slider so long as the total force fi< fsi ,
where fsi is a threshold value. Above the
threshold the contact detaches from the slider and slips relative to it for a
delay time τd after which it stops and
attaches again to the slider; at this moment its stretching is determined from the condition that
the total force fi on the contact is equal
to the "backward" force fb~ 0. The force F from the interface
acting on the slider is the sum of the forces from the pinned contacts, fi(sub)= kixi (recall that xi is the stretchings of the
contact and ki is its elastic constant), plus additionally the sum of drag forces from the detached/sliding
contacts, fi(drag)
= −miηi [v−dxi(t)/dt
], where v(t) = dX(t)/dt is the
slider velocity, mi is the mass of the
contact and ηi is the
corresponding damping coefficient (e.g., the "viscosity" of the molten
lubricant).
Because the slider is rigid, at any abrupt change of its motion, e.g., at the onset or stopping of motion, it will undergo vibrations with the setup frequency ΩS= (K/M )1/2, which cannot decay and therefore will disturb the results. In a real system, these oscillations will be attenuated because of internal friction inside the setup (i.e., due to phonon damping in the slider, when its bottom surface oscillates relative the top one). To incorporate such a damping, we introduce a viscous damping coefficient ηS for the slider motion relative its average velocity, so that finally the slider motion equation is
|
(S40) |
|
(S41) |
Model parameters. In
simulation we used the EQ algorithm (the ME approach
leads to the same results). For the sake of quantitative results, we extracted model parameters from
the experiment of Klein (J. Klein, Phys.Rev.Lett. 98 (2007) 056101),
where the OMCTS (octamethylcyclotetrasiloxane) lubricant film of the thickness h = 3.5×10
Second, we have to take into
account the elasticity of the slider which may lead to the elastic instability
(for more details see
![]() ).
The master equation allows us to calculate the force F(X) when the bottom of the solid block is displaced by
X, but actually we don't control X. The displacement is caused
by a shearing force Fd= K (Xd− X) applied on the top
of the solid block which displaces the top surface by Xd. The total force applied to the bottom
of the sliding block, which determines its displacement X, is
the sum of the applied force and the force from the interface, Ftot= K (Xd−X)
− F(X). This force can be viewed as deriving from the potential
).
The master equation allows us to calculate the force F(X) when the bottom of the solid block is displaced by
X, but actually we don't control X. The displacement is caused
by a shearing force Fd= K (Xd− X) applied on the top
of the solid block which displaces the top surface by Xd. The total force applied to the bottom
of the sliding block, which determines its displacement X, is
the sum of the applied force and the force from the interface, Ftot= K (Xd−X)
− F(X). This force can be viewed as deriving from the potential
|
(S42) |
A necessary condition for smooth sliding is that Xd and X grow together with Xd− X = B, where B is a constant that measures the shear strain of the solid block during the sliding. It is determined by the condition ∂Veff/∂(Xd−X) = −∂Veff/∂X = 0, which simply means that the total force on the interface vanishes. Smooth sliding also requires this state be stable,
|
(S43) |
If we start from relaxed asperities, in the early stage of the motion F(X) is a growing function of X (see Fig.S18), and then it passes by a maximum when some contacts start to break and reform at lower asperity stress. As a result F'(X) = dF/dX becomes negative. Depending on the value of K, two situations are possible. For large K (K > K*= − max F'(X), stiff block) F'(X) never falls below −K and the smooth sliding is a stable steady state. For small K (K < K*, soft block) F'(X) can become smaller than −K so that the stability condition (S43) is no longer valid (this is the well-known elastic instability, e.g., see T.Baumberger and C.Caroli, Advances in Physics 55 (2006) 279). The instability may cause Xd− X to change abruptly by a breaking of all contacts and a quick slip of the block before the contacts reform with relaxed asperities. If the process repeats itself, we have the stick-slip motion. The master equation, which gives F(X), can be used to compute the period of the stick-slip. However, the existence of a stick slip is not only determined by the stiffness K of the block, but also by the distribution Pc(x) of the static thresholds and the time of contact reforming, as is described below.
|
|
Figure S18: The force F∞(X) = −F(X) versus the displacement X for Δfs/fs= 0.2 (fs= 1 and Nk = 1). The oscillations are due to the alternate prevailing of contact breaking (F drops) and contact reforming (rises).
At the beginning F(X) grows linearly with X, F(X)= NkX, until it reaches a value ~ Fs− ΔFs. Then the growth reduces and changes to a decrease during a displacement x*~ Δfs/k till almost all contacts reborn. Then the process repeats with a smaller amplitude, and so on.
|
Thus, if the slider is soft enough, K < K*, its motion becomes unstable at the point Xc, where Xc is the (lowest) solution of the equation F'(X) = −K (see Fig.18). Let this occur at the moment tc. After the unstable point, t > tc, the motion equation in terms of ΔX = X − Xc and Δt = t − tc is
|
(S44) |
with the initial condition ΔX = 0 and dX/dt = vd at Δt = 0. In the EQ model with the continuous distribution of static thresholds, the function F(X) near the point Xc can be approximated as F(X) ≈ F(Xc) + F'(Xc) ΔX + (1/2)F''(Xc) ΔX2 + (1/6)F'''(Xc) ΔX3, so that
|
(S45) |
Introducing the dimensionless variables x = K (X − Xc) / Fs and τ = ΩS(t − tc), we obtain the following equation for the slider coordinate:
|
(S46) |
where
|
Solution of Eq.(S46) should be found with the initial condition x(0) = 0 and dx(τ)/dτ|τ=0= D1. At short times, τ << 1, the solution has the form x(τ) ≈ D1τ + (1/6) D1τ3. Thus, as X(t) grows at t > tc, the spring force quickly drops during a slip time τs≈ α/ΩS in the form
|
where α = (6FsΩS /Kvd)1/3 (α ≈ 2.21 for the chosen set of parameters). Numerical solution of Eq.(46) is shown in Fig.S19.
|
|
Figure S19: Drop of the spring force ΔFd(τ)/Fs= D1τ − x(τ) versus dimensionless time τ = ΩS (t − tc) for the slider motion after the unstable point (X > Xc) according to numerical solution of Eq.(S46) (black curves, sequential
breaking of contacts) or Eq.(S47) (blue curves, instant melting of the
lubricant) for Δfs/fs= 0.01
(solid curves; D0= 0.94, D1= 2.1×10
|
On the other hand, if the whole lubricant film melts instantly at t = tc, then for t > tc we have F(Xc+ΔX) = Mη d(ΔX)/dt, and the motion equation in dimensionless variables takes the form
|
(S47) |
where D0= − Fd(Xc)/Fs. Its solution for τ <<1 is x(τ) ≈ D1τ + Bτ2, so that the spring force drops as
|
with B = (1/2)(D0− ηD1/ΩS). This gives the slip time τs≈ β/ΩS with β = [2/(D0− ηD1/ΩS)]1/2. Numerical solution of Eq.(S47) is shown in Fig.S19. One can see that in this case the slip time is much shorter; however, using artificially huge values for η, one may make τs as large as desired (see discussion).
A typical example of stick-slip
motion of the EQ model for the chosen set of parameters is presented in
Fig.S20. It is very similar to that observed experimentally, including the
large initial stick spike and subsequent stick spikes of smaller amplitude
(e.g., compare Fig.S20 with Figs. 1 and 2 in Klein's paper, see
![]() ).
).
|
|
Figure S20: Calculated spring force in the stick-slip regime. The inset shows the detail of a slip, with the sudden force drop and mechanical ringing oscillations. |
Details of the slip are shown in Fig.S21. During the slip time τs, the slider velocity grows up to a value v ~ ΩSFs/K. As the slider accelerates, the contacts break, the number of detached contacts grows, and the force F(t) on the slider from the contacts drops from Fd(tc) to zero. After the delay time τd , the contacts reborn, and F(t) grows as F(t) = Ct with the rate C = Nkvt back to the value ~Fd(t). Therefore, the force F oscillates with a period τB≈ Fs/Nkv ≈ K/NkΩS. Such oscillations exist provided τB< τs, or K < Nk.
|
|
Figure S21: Details of the slip shown in Fig.S20.
(a) The slider velocity,
(b) the spring force Fd (red dashed curve) and the force F from the contacts (black solid curve), and
(c) the number of detached contacts Nd as functions of time.
|
Third, let us consider the
role of delay time. One may think that the elastic instability will result in
stick-slip motion. However, the condition K < K* is the
necessary but not sufficient one for stick-slip; the second necessary condition is a nonzero delay time, τd> 0.
This is clearly demonstrated in Fig.S22: if τd= 0,
the system still approaches the smooth sliding (for more details see
![]() ).
).
|
|
Figure S22: Spring force Fd(t) for different values of the delay time τd.
Despite the soft spring constant K = 97 N/m << K*= 4.34×104 N/m, stick-slip is only found for sufficiently large τd |
The subsequent (after the slip)
motion of the slider depends on a value of the parameter τd. If τd > ΩS
If we neglect ringing oscillations,
then the dependence Fd versus vdt is "universal". Thus, if the velocity is so
small that τss >>
ηS
Role of threshold's dispersion. The system behavior (either stick-slip or smooth sliding) is controlled by the dispersion Δfs. Indeed,
|
(S48) |
Thus, if Δfs is so small that K*> K, then the motion corresponds to stick-slip; otherwise the smooth sliding regime is achieved. In the stick-slip regime, an increase of Δfs leads to the decrease of the period τss of stick-slips as demonstrated in Fig.S23. The time τs of the F(t) drop during slip also increases with Δfs, but this effect is rather small.
|
|
Figure S23: Dependences Fd(t) for different values of the dispersions Δfs
|
Finally, note that the ratio Δfs/fs should decrease with the time of stationary contact due to aging of contacts; namely this aging is responsible for the transition from stick-slip to smooth
sliding with the increase of driving velocity as described in next section
![]() .
.
Role of slider
elasticity. Above
we have assumed that the slider is a rigid body; in a real setup, however, both the
slider
mass and its elasticity are distributed through the slider.
 One
may think that in this case, only the most bottom atomic layer of the slider
starts to move at the onset of slip. Therefore, a characteristic frequency will
be determined by the mass Ml of the layer and
its elastic constant Kl ; this could lead to a much
higher (atomic scale) frequency. A similar question
– which mass, either the total mass M or the layer
mass Ml , defines the time scale of the
system – appeared in the problem of minimal
velocity for the atomic-scale smooth sliding.
As was
proven, when the slider velocity decreases, first the most bottom layer
stops; then the stopping wave emerges and takes away the kinetic
energy of the slider. In a result, the time scale of that problem is determined
by the layer mass Ml , and the minimal
velocity is of atomic-scale order (~m/s).
One
may think that in this case, only the most bottom atomic layer of the slider
starts to move at the onset of slip. Therefore, a characteristic frequency will
be determined by the mass Ml of the layer and
its elastic constant Kl ; this could lead to a much
higher (atomic scale) frequency. A similar question
– which mass, either the total mass M or the layer
mass Ml , defines the time scale of the
system – appeared in the problem of minimal
velocity for the atomic-scale smooth sliding.
As was
proven, when the slider velocity decreases, first the most bottom layer
stops; then the stopping wave emerges and takes away the kinetic
energy of the slider. In a result, the time scale of that problem is determined
by the layer mass Ml , and the minimal
velocity is of atomic-scale order (~m/s).
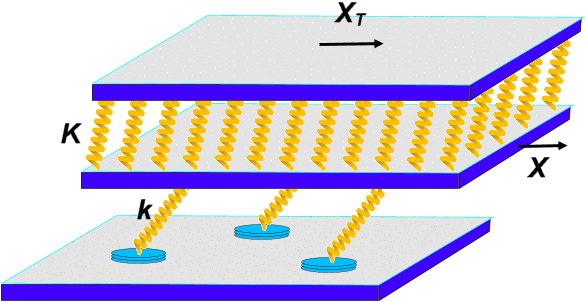
Now, however, the situation is just opposite. To show this, let us consider the slider as consisting of Nl layers, each of the mass Ml= M/Nl, elastically coupled by springs of the elastic constant Kl= KNl (see inset in Fig.S24). Indeed, if we fix the bottom layer and apply a force F to the top layer, then the latter will shift on the displacement ΔX = ∑l=1Nl ΔXl , where ΔXl = F/Kl , so that ΔX = F/K as before. Now let the top layer be driven with the velocity vd, while the bottom layer be in frictional contact with the bottom substrate. The dependence of the elastic force in the slider on time, obtained with simulation for two different values of Nl , is shown in Fig.S24 (note that now we may not use the artificial damping ηS , because internal degrees of freedom are included). As seen, the slip kinetics is almost independent on the number of layers Nl and is determined by the minimal slider mechanical frequency ΩS.
|
|
Figure S24: Slip kinetics for the nonrigid slider consisting of Nl= 16 (red dashed) or Nl= 64 (solid curve) layers (top inset shows the whole stick-slip cycle; ηS= 0). Bottom inset shows the layered model of the slider: the first layer is in contact with the bottom substrate, while the last layer is moved with the velocity vd |
The frequency ΩS can be found with the help of elastic theory. Let the slider have a cylinder shape of height L and radius r, and let it be characterized by the section S = πr2, inertial momentum I = πr4/4, mass density ρ and Young modulus E. If the cylinder foot is fixed and a force F is applied to its top, the latter will be shifted on the distance ΔX = FL3/3EI (the problem of bending pivot, see Sec.20, example 3 in the Landau and Lifshitz (LL) textbook). Thus, the effective elastic constant of the slider is K = 3EI/L3. The minimal frequency of bending vibration of the pivot with one fixed end and one free end, is given by ΩS= (3.52/L2)(EI/ρS)1/2 (see Sec.25, example 6 in LL). Taking M = ρSL, we finally obtain ΩS≈ 2.03√(K/M).
Finally, let us consider the role of interaction between the
contacts (here we present a qualitative analyses only; for an accurate
consideration of the problem see
![]() ). A concerted, or synchronized breaking
(triggering) of contacts may be studied numerically only within the earthquakelike model, it cannot be included accurately in the ME
approach (although it may be incorporated indirectly in a mean-field fashion by
renormalization of the distributions Pc(x) and
R(x), see
). A concerted, or synchronized breaking
(triggering) of contacts may be studied numerically only within the earthquakelike model, it cannot be included accurately in the ME
approach (although it may be incorporated indirectly in a mean-field fashion by
renormalization of the distributions Pc(x) and
R(x), see
![]() ).
).
The elastic interaction between contacts separated by a distance r is described by the pairwise potential V(r) = g/r3, where g is a constant. Using ∂V/∂x = V'(r) ∂r/∂x, V'(r) = dV/dr = −3g/r4 and ∂r/∂x = x/r, we obtain that the force acting on the ith contact from its nearest neighbors (NN), is equal to
|
The interaction becomes important when g/a3 ~ fsa, where a is the average distance between NN contacts; therefore, it is interesting to check, how the system behavior changes with the dimensionless parameter ξ = g/(fsa4).
The interaction between the contacts works roughly in the same way as the dispersion Δfs: the stronger is the interaction, the wider is the range of model parameters where stick-slip operates. To demonstrate this effect, we calculated the system kinetics with increasing strenght of the interaction (ξ = 0 to 0.3) for softer contacts (kN = 200 N/m) and a larger dispersion of the thresholds (Δfs/fs= 0.3). The results are presented in Fig.S25: for these parameters, the system quickly goes to smooth sliding for noninteracting contacts (Fig.S25a), but demonstrates stick-slip for a strong interaction ξ = 0.3 (Fig.S25d).
|
|
|
|
Figure S25: Dependence of the spring force Fd(t) on time for different strengths of the interaction ξ for kN=200 N/m and Δfs/fs= 0.3. |
Figure S26: Dependence of the number of broken contacts Nd(t) on time during slip for different strengths of the interaction. Parameters as in Fig.S25. |
Details of the slip are shown in Fig.S27: without interaction, contact's detaching is sequential, while for a strong interaction, all contacts detach simultaneously, and the force F abruptly drops to zero. This is clearly demonstrated in Fig.S27 (compare panels (a) and (d)).
|
|
Figure S27: The spring force Fd(t) (red dashed) and the force from contacts on the slider F(t) (black solid curve) during slip for noninteracting (a) and strongly interacting (d) contacts. Parameters as in Fig.S25.
|
The interaction may lead to avalanches as was observed in the EQ simulation: for ξ = 0 the contacts break sequentially, one after another, while for ξ > 0 one contact may stimulate the breaking of nearest contacts, and the average size of avalanche increases with ξ as demonstrated in Fig.S26. For a large strength of interaction, ξ = 0.3, the avalanche occupies the whole system (Fig.S26d).
In tribological community there exists an opinion that the viscosity of a thin confined film is many orders of magnitude higher than the bulk viscosity (P.A.Thompson, M.O.Robbins, G.S.Grest, Israel J.Chem. 35 (1995) 93; H.-W.Hu, G.A.Carson, S.Granick, Phys.Rev.Lett. 66 (1991) 2758). For example, considering the drop of the spring force during slip, Klein (J.Klein, Phys.Rev.Lett. 98 (2007) 056101) came to the conclusion of "high viscosity" of the molten lubricant film, η ≈104ηOMCTS. So large viscosity of a thin film, however, has no reasonable explanation. The cases of a single or two molecular layers confined between two planar surfaces are exceptional in the sense that properties of such films are far from their bulk ones. But already a three-layer film, if it is melted (liquidized) during slips, should exhibit properties not very different from the bulk ones, as follows from almost all MD simulations.
In our model with a distribution of static thresholds, the time τs of F(t) drop is almost solely determined by the setup frequency ΩS. This time remains approximately unchanged even if we increase the model parameter η (which corresponds to the film "viscosity") in 105 times as demonstrated in Fig.S28.
|
|
Figure S28: Dependence of the spring force Fd(t) on time for different values of the lubricant viscosity η.
|
The conclusion about a huge viscosity of a thin confined film is based on the assumption that the lubricant film is (ideally) homogeneous and, at the onset of slip, the whole film melts simultaneously so that the further slip proceeds with a liquid film. When the film instantly melts, the force F on the slider from the interface abruptly drops to the viscous force (which starts from zero being proportional to the slider velocity), while the force from the driving spring remains unchanged at the beginning. Therefore, if the slip is viewed as a uniform, massive lubricant melting event, then the limiting factor would be the lubricant's viscosity, and in that case very large viscosity values for the lubricant's viscosity are required, 104 to 107 times higher than that of the bulk lubricant, to explain experimental results.
However, this assumption has neither experimental nor theoretical support. From surface science physics it is known that a thin film may hardly be homogeneous on a meso- and even nanoscale, as well as the surfaces themselves are not ideally crystalline on these scales. Generally, a film consists of domains with different orientation or even different structure and, therefore, are characterized by different threshold stress yields. Thus, it is reasonable to assume that the film does not melt and begin to slide all at ones, but different domains start to slide one by one, as described by the EQ model. In this case, the decrease of F is gradual owing to consequent breaking (melting) of different contacts (domains), and this approach describes the X(t) dependences observed experimentally.
The mechanism of slip onset (either
sequential breaking of the contacts or the instant melting of the lubricant
film) determines details of the slip kinetics which in principle may be resolved
with SFB experiments. The order of magnitude of the slip time, however, in both
cases is determined by the setup mechanical frequency ΩS. In our model adapted to the SBF
setup, the sliding mass M is concentrated at the end of the
spring, i.e., the slider plus spring form a usual pendulum. A pendulum is
characterized by two characteristic times –
the
inverse of its frequency, Ω
The frequency of ringing vibrations
after the slip is either ΩS (if F(t) oscillates around zero in the case of τd>
Ωs
Notice also that, in the case of dF(v)/dv < 0 which emerges because of contact's aging, the regimes of stick-slip and smooth sliding may be separated by a regime of irregular (chaotic) motion due to inertia effects.
See also:
O.M. Braun, Europhys. Lett. 109 (2015) 48004 "Stick-slip vs. smooth sliding in the multicontact interface"
O.M. Braun and E. Tosatti, Philosophical Magazine 91 (2011) 3253-3275 "Kinetics and dynamics of frictional stick-slip in mesoscopic boundary lubrication"
O.M. Braun and E. Tosatti, Europhys. Lett. 88 (2009) 48003 "Kinetics of stick-slip friction in boundary lubrication"
Last updated on March 3, 2015 by O.Braun. Translated from LATEX by TTH