Friction on Mesoscopic Scale

Generalizations  

 

Delay in contact formation goto top

More rigorously, in Eq.(5) we have to use ΔQ+(x; X+ΔXm), where ΔXm= vτd (v is the driving velocity) and τd is a "delay" time, i.e., the time of break-formation (e.g., melting-freezing in the case of liquid lubricant film) of a new contact. Simulations show that τd> 102τ0, where τ0~ 10–13 sec is a characteristic period of atomic oscillation in the lubricant. Above we ignored the delay effect; in this case ΔXm= ΔX,  and we may drop the +ΔX  because it is a second order correction since it appears in a term which is already a correction to Q.
Now let us include the delay in the master equation. With this, the integro-differential equation (6) is to be modified to the form
 
∂
Q
 (x; X)
∂x		  +  
∂
Q
 (x; X)
∂X		  +  P(x)
Q(x; X)  =  R(x)
   ⌠
 ⌡ 		∞

-∞		 dx' P(x') Q(x'; X−ΔXm) .    
(21)
Now, however,  Q(x; X)  corresponds to the total number of unbroken contacts, which is not conserved anymore. When the asperity breaks, it is not in contact with the substrate during the time τd until the contact will be formed again. Typical dependences F(X) for different values of the delay time are shown in Fig.6. The kinetic friction force in smooth sliding depends now on prehistory of the contacts (for details see and ). If one starts from the same initial configuration, the final force Fk is the lower, the larger is the delay time.
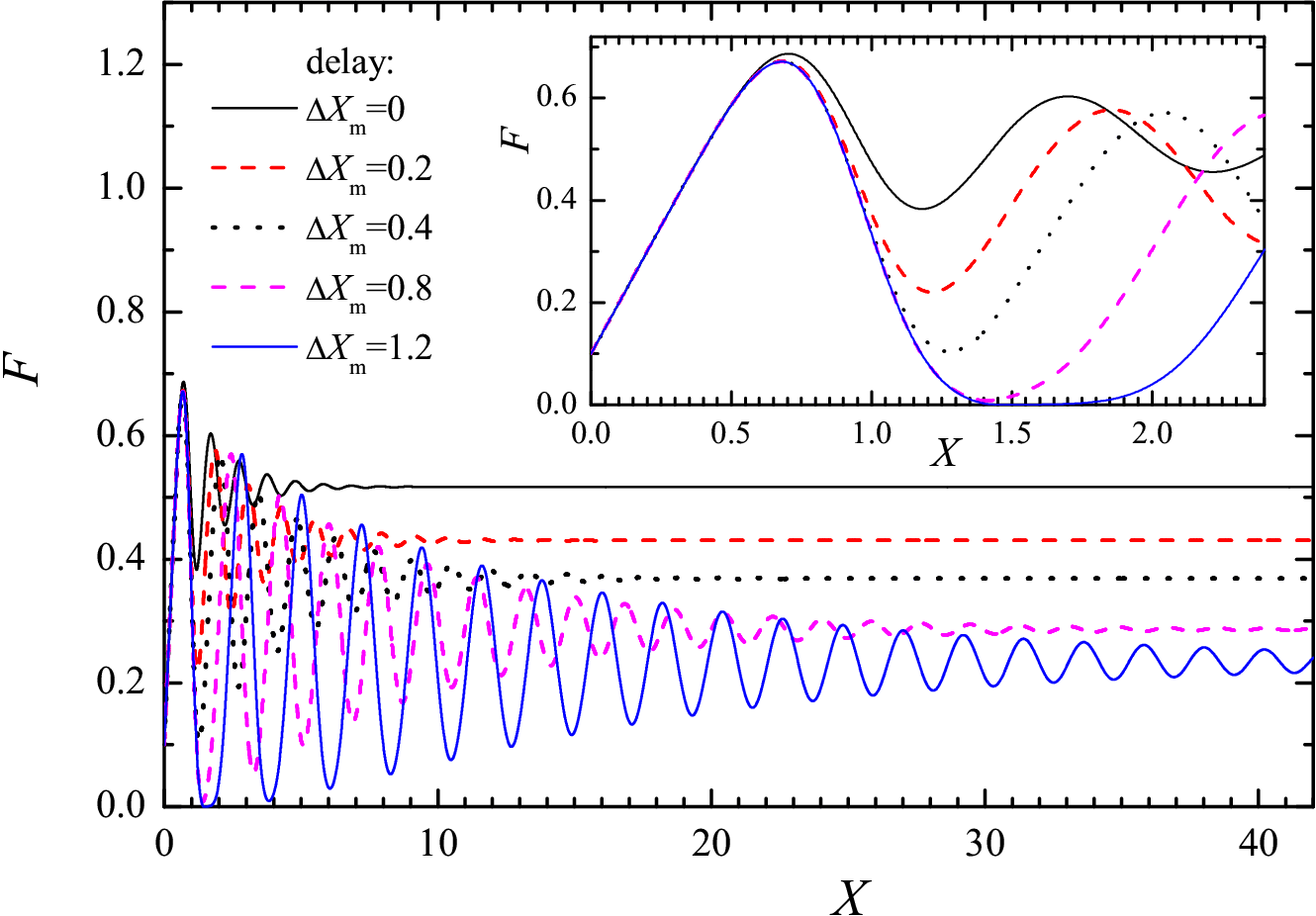Figure 6: The dependences F(X) for different delay times. The distribution Pc(x) is Gaussian with xs= 1 and σs= 0.2, the initial distribution Qini(x) is Gaussian with xini= 0.1 and σini= 0.025.

Aging of junctions goto top

Now let us take into account the aging of contacts (see also and for more details). Experiments as well as MD simulations indicate that the static friction force grows with the time of stationary contact (the waiting time tw, i.e., the duration of static contact prior to sliding). Thus, if the newborn contacts are characterized by a distribution Pci(x) with the average xsi and dispersion σsi , then typically xs grows while σs decreases with time, and at t → ∞  the distribution  Pc(x, t)  approaches a distribution Pcf(x) with xsf  > xsi and σsf < σsi. If we assume that the evolution of Pc(x) corresponds to a stochastic process, then it should be described by the Smoluchowsky equation

 

∂Pc(x, t)

∂t

 = D Lx Pc(x, t) , 

  where   

  

Lx

≡

∂

∂x

 

[

B(x) + 

∂

∂x

]

,

(22)

the "diffusion" parameter D describes the rate of aging, B(x) = dU(x)/dx, and the "potential" U(x) is defined by the final distribution, Pcf (x) ∝ exp[−U(x)]  so that

B(x) = −

dPcf (x) /dx

Pcf (x)

.

(23)

Then, the equation ∂Pc/∂t = DLxPc naturally leads to the growth of the average static threshold from xsi to xsf  with the time of stationary contact, as widely assumed in earthquakelike models of friction (e.g., see Eq.(Fs) in previous Chapter). At the same time, the contacts continuously break and reborn when the substrate moves, as described by third and forth terms in Eq.(6). Combining both the processes together, we come to the system of three equations:

 

 

 

 

∂Q(x; X)

∂x

 +  

∂Q(x; X)

∂X

 +  P(x; X) Q(x; X)  =  δ(x)

⌠
 ⌡

∞

-∞

dx' P(x'; X) Q(x'; X) ,

 

 

 

 

 

∂Pc(x; X)

∂X

 − DX  Lx Pc(x; X)  +  P(x; X) Q(x; X)

 =  Pci(x)

⌠
 ⌡

∞

-∞

dx' P(x'; X) Q(x'; X) ,

 

 

    

 

 

Pc(x; X)  =  P(x; X) exp [ −

⌠
 ⌡

x

0

dξ P(ξ; X)

 

] ,

 

(24)

where DX ≡ D/v  and v = dX(t)/dt is the driving velocity. Thus, in the case of high driving  (v → ∞, DX → 0)  we obtain the previous behavior with Pc(x) = Pci(x), in the case of low driving  (v → 0, DX → ∞)  we again observe the same type of behavior but with Pc(x) = Pcf (x), and in the case of  0 < DX < ∞  we have an interplay of two processes – the aging which moves Pc(x) to Pcf (x), and the breaking/reborn process which returns Pc(x) to Pci(x)  (see Fig.7). 

Figure 7: Evolution of Pc(x) due to two concurrent processes: the first is the aging of asperities from the initial (fresh) distribution Pci(x)  (Gaussian with xsi= 0.5 and σsi= 0.05) to the final distribution Pcf (x)  (Gaussian with xsf = 1 and σsf = 0.02), and the second is the break/reborn process.

DX ≡ D/v = 5×10–4,  the initial distribution Qini(x) is Gaussian with xini= 0.1 and σini= 0.025. The curves are plot with the increment ΔX = 0.05.

 

 

In the result, the friction force F now depends on the sliding velocity as shown in Fig.8.

Figure 8:

 

(a) The final distribution Qs(x) for five values of the parameter  DX ≡ D/v:  10–5 (circles), 10–4 (up triangles), 3×10–4 (crosses), 10–3 (down triangles), and 10–2 (diamonds).

 

(b) The corresponding distributions Pc(x); larger circles show the initial distribution Pci(x) (red) and the final distribution Pcf (x) (blue).

 

Inset demonstrates the dependence of the kinetic friction force F  in the steady state on the driving velocity v.

Here ‹ki› = 1, Pci(x) is Gaussian with xsi= 0.5 and σsi= 0.1, and Pcf (x) is Gaussian with xsf = 1 and σsf = 0.01.

 

Note: because typically  xsi< xsf , the force F decreases when v grows, so that dF(v)/dv < 0; that may lead to instability of the smooth sliding regime

 

 

 

If the sliding block is not rigid, K < ∞, the system will demonstrate either stick-slip or smooth sliding depending on the distribution  Pc(x); in this case the effect of contact's aging must lead to the transition from stick-slip to smooth sliding with the increase of sliding velocity (for details see and ).

Note: in the case of contact of rough surfaces, the physical mechanisms of contact aging, according to Baumberger and Caroli (2006), are the following: the first (and more important) mechanism is due to geometrical aging, or the increase of contact area at the asperity, and the second, due to structural aging, or restructuring of the contact. The value of the parameter D in Eqs.(24) may be estimated from experiments which show that in most cases the average static threshold μs= Fs/Fload grows logarithmically with the waiting time tw,  dμs/d(ln tw) ≈10-2.

 

Role of temperature goto top

In a general case, the parameter D in Eqs.(24) and, therefore, the rate of contact's aging depends on the system temperature T. Typically, the rate increases with T according to Arrhenius law, D ∝ exp(−ε/kBT), where kB is Boltzmann's constant and ε is an activation energy for this process.
Another effect of a nonzero temperature is connected with the change of the rate of contact breaking P(x) in the master equation (6). Indeed, for a single contact with the static threshold xs at zero temperature, the breaking rate is zero for x < xs. But when T > 0, the contact may relax due to a thermally activated jump before the threshold xs is reached. The rate of this process is
dQ(t)/dt = h(x; xs) Q(t) ,     x < xs .
(25)
For the set of contacts, Eq.(25) is to be generalized to 
dQ(t)/dt = H(x) Q(t) ,   where   H(x) = ⌠
 ⌡ 		∞

x		 dx' h(x; x') Pc(x') .
(26)
If we put X = vt, then the thermally activated jumps can be incorporated in the master equation, if we will use, instead of the zero-temperature rate P(x), the rate coefficient PT(x) defined as
PT (x) = P(x) + H(x)/v .
(27)
The rate of thermally activated jumps h(x; xs) in Eq.(25) can approximately be determined by the Kramers relation. Let V(x) be the elastic energy of the contact, and ΔE(x; xs) = V(xs) − V(x), the activation energy for the contact rupture. For "soft" ("weak") contacts, when ΔE(0; xs) > kBT, the rate  h(x; xs)  is given by
h(x; xs) ≈ ω exp[ −ΔE(x; xs)/kBT ] ,
(28)
where ω is a prefactor corresponded to the attempt frequency (for the overdamped motion of contacts ω ≈ ω02/2πη with the characteristic frequency ω02 ~ k/m ~ c2/A  and the damping coefficient η ~ c/√A which gives ω ~ c/2π√A ~ 1010 s–1).  If we set  V(x) = 1/2kx2,  then the activation energy takes the form
ΔE(x; xs) = 1
2		 k (xs2− x2) ≈ k xs(xs− x) ,
(29)

and the function H(x) in Eq.(27) is determined by

H(x) = ω exp(kx2/2kBT )

⌠
 ⌡

∞

x

dξ Pc(ξ) exp(-kξ2/2kBT ) .

(30)

On the other hand, for "stiff", or "strong" contacts, when ΔE(0; xs) >> kBT, we have to substitute in Eq.(28) for the activation energy the expression ΔE(x; xs) = ΔE(0; xs) (1−x/xs)3/2, and also to renormalize the prefactor ω, ω → ω (1−x/xs)1/2. In this case the function H(x) is to be calculated as

H(x)  =  ω 

⌠
 ⌡

∞

x

dξ Pc(ξ)

(

1−

x

ξ

)

1/2

 

exp

[

−

kξ2(1−x/ξ)3/2

2kBT

]

.

(31)

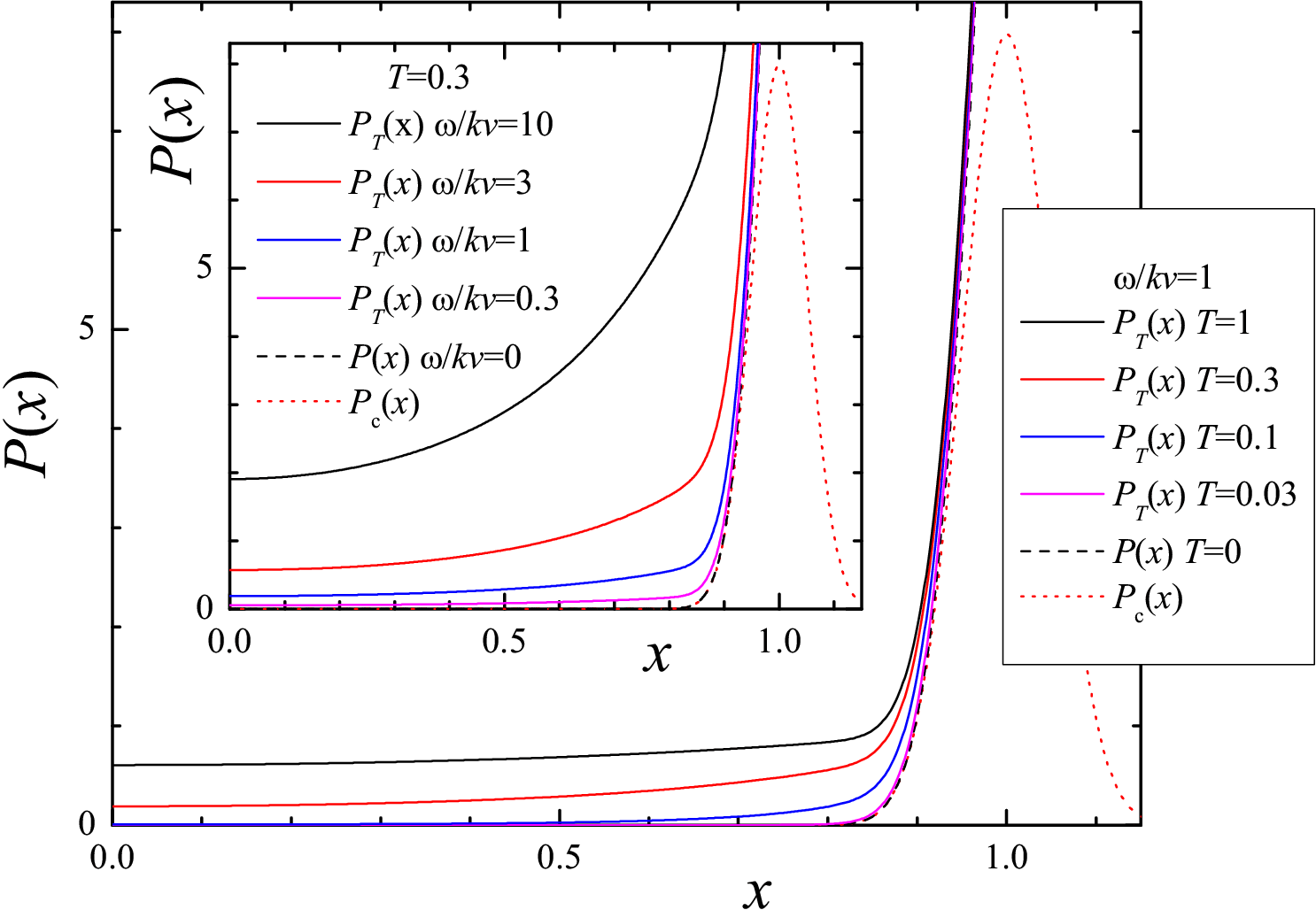
The contribution (30) or (31) to the rate PT(x) leads to appearance of a low-x tail. Its height grows with temperature as well as with decreasing of the driving velocity v as demonstrated in Fig.9. The increase of temperature leads to a shift of the distribution Q(x) to lower values, so that the friction force decreases when T grows. The effect is the larger, the lower is the sliding velocity as shown in Fig.10. In the limit v → 0, all contacts will finally break if T > 0, so that Qs(x) → δ(x) and Fk→ 0; in this limit we have "smooth sliding" corresponded to creep motion of contacts.

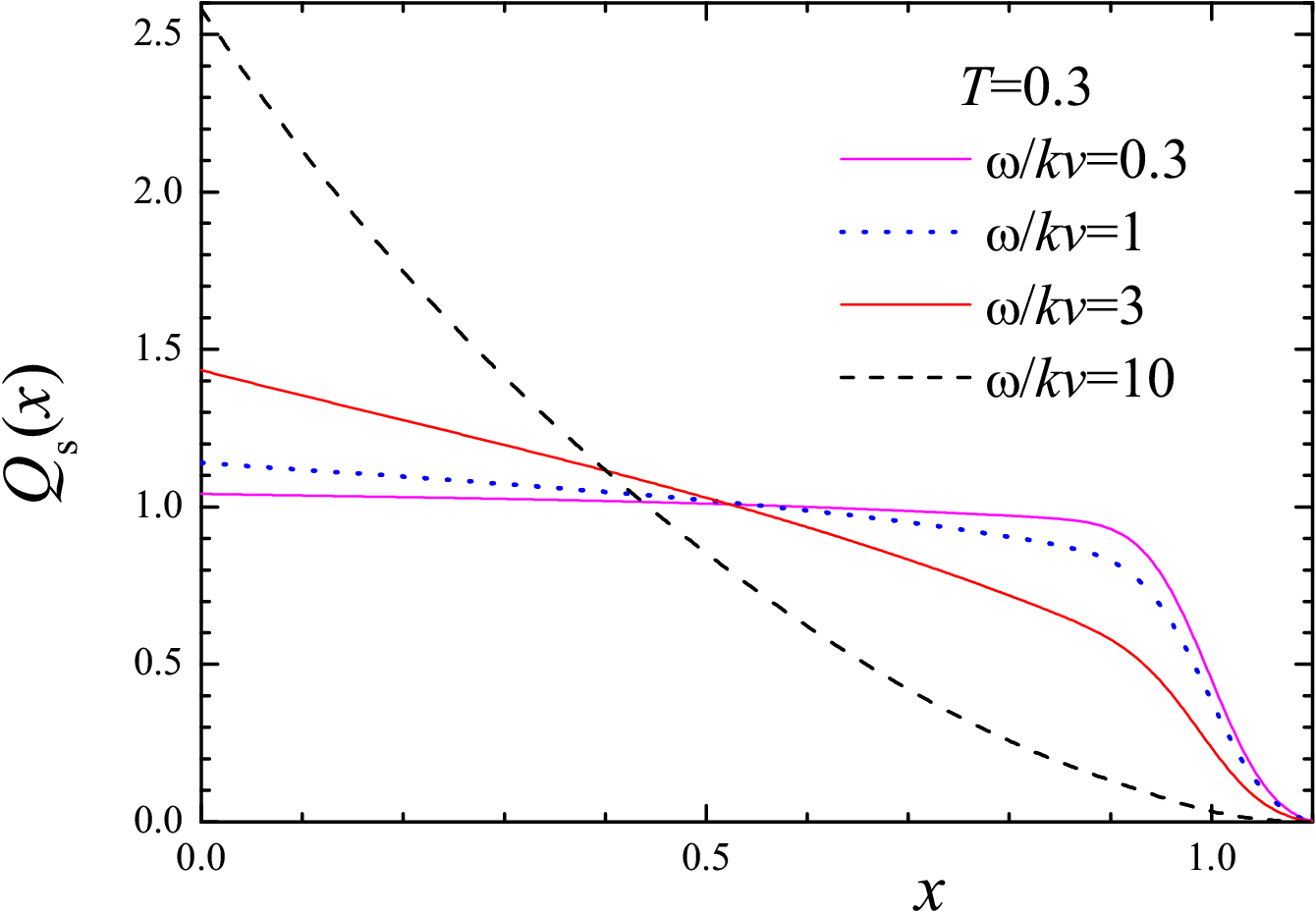Figure 9: The rate PT(x) for soft contacts at different temperatures T = 0 to 1 for a fixed velocity ω/kv = 1, and (inset) at different velocities, ω/kv = 0 to 10, for a fixed temperature T = 0.3. Dotted curve shows the distribution Pc(x) (Gaussian with xs= 1 and σs= 0.05). Figure 10: The steady-state distribution Qs(x) for T = 0.3 and different velocities  (ω/kv = 0.3, 1, 3 and 10) for soft contacts. The distribution Pc(x) is Gaussian with xs= 1 and σs= 0.05.
The dependences Fk(T) for different values of the sliding velocity in the smooth sliding for soft and stiff contacts are presented in Fig.11. The friction force decreases when T grows and tends to zero when T → ∞. Fig.11b demonstrates the dependence Fk(v); the force Fk monotonically increases with v,  approaching the T = 0 limit when v → ∞ (according to Persson,  Fk(v) ∝ ln v  in the low-velocity limit, and Fk(v) − F(∞) ∝ −ωT2/kv  in the high-velocity case). Thus, at T > 0 the force Fk increases with the velocity, i.e., the dependence F(v) is opposite to that emerged due to aging of contacts. Note that the inequality dF(v)/dv > 0 stabilizes the smooth sliding regime. However, experiments show that the temperature-induced velocity-strengthening may dominate over the aging-induced velocity-softening at high velocities only, v > 10 − 100 μm/s.

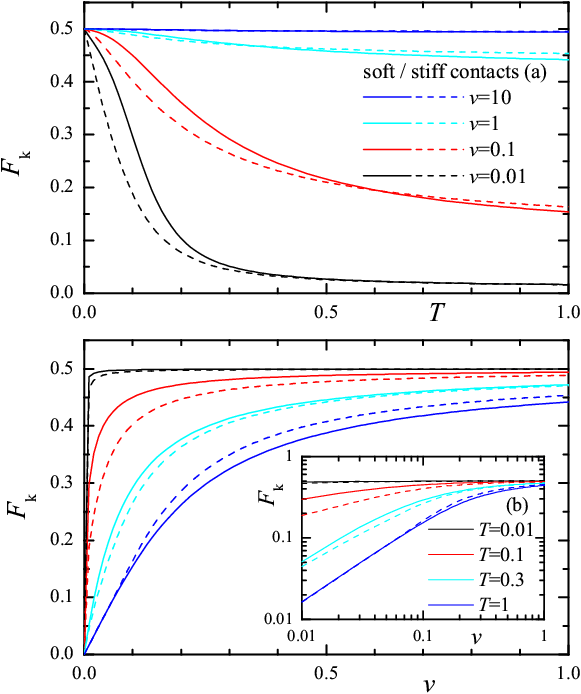
Figure 11: (a) Dependence of the kinetic friction force Fk in the steady state on temperature for different velocities v = 0.01, 0.1, 1 and 10.  (b) Fk(v) for different temperatures T = 0.01, 0.1, 0.3 and 1; inset shows the same in log-log scale. Solid curves are for soft contacts, and broken curves, for stiff contacts. The distribution Pc(x) is Gaussian with xs= 1 and σ = 0.05; ω/k = 1.

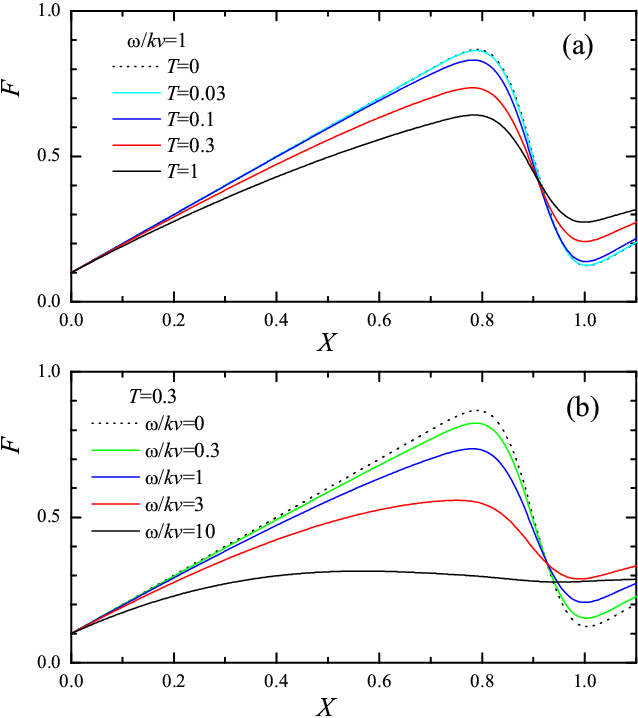
Figure 12: The dependences F(X) for short X. 

(a) F(X) for different temperatures T = 0, 0.03, 0.1, 0.3 and 1 at the fixed velocity ω/kv = 1; 

(b) F(X) for different velocities v, ω/kv = 0, 0.3, 1, 3 and 10 at the fixed temperature T = 0.3.

Nonzero temperature influences on the dynamics of approaching to the steady state (see Figs.12 and 13). The higher is temperature and/or the lower is velocity, the lower is the static friction force Fs determined by the first maximum of F(X), and the faster F(X) approaches to the steady-state smooth sliding. Also it is important to consider the first cycle of the F(X) dependence, which defines the lowest value of F'(X).  The higher is temperature, the lower is the extremum of F'(X)  (see Fig.12a), so that the larger is the interval of model parameters where the smooth sliding regime operates. At the same time, the higher is driving velocity (Fig.12b), the smaller is the lowest value of F'(X),  so that the narrower is the interval of model parameters where the smooth sliding regime operates (also see ). Thus, we come to a surprising conclusion that at T > 0  the decreasing of pulling velocity may lead to the transition from stick-slip to smooth sliding, i.e., the scenario just opposite to the conventional one (in fact, stick-slip shoud exist for an interval of driving velocities and disappear low lower and higher velocities, see ).

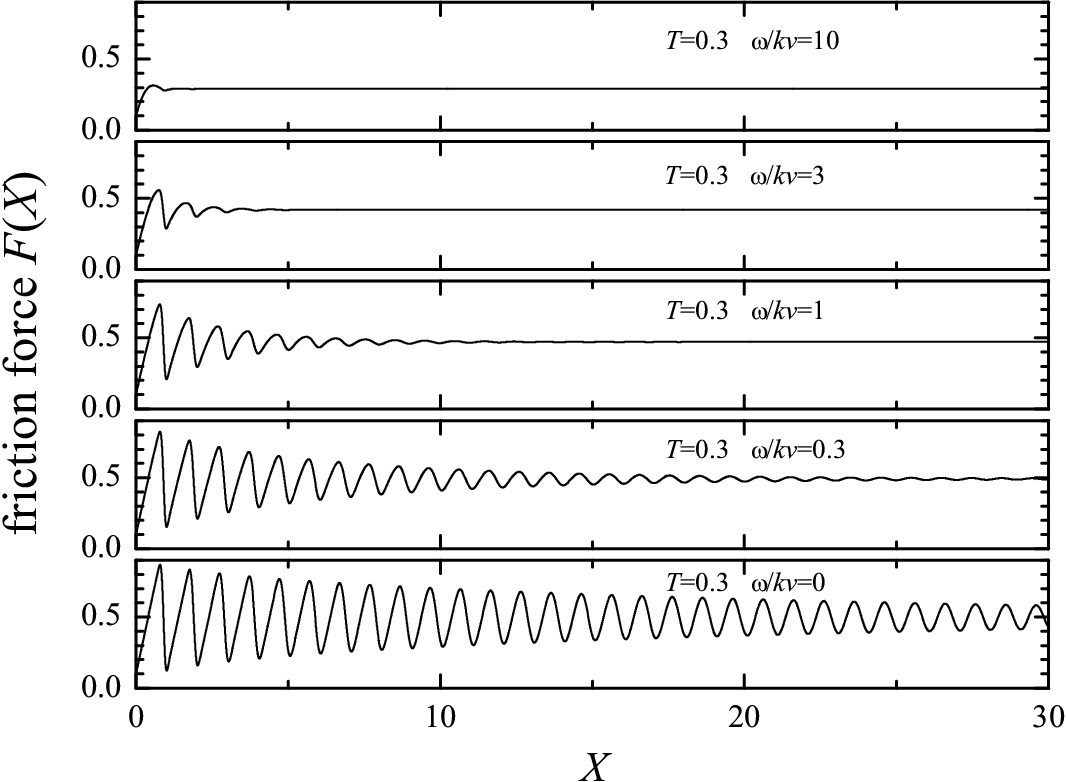
Figure 13: The dependences F(X) for T = 0.3 at different driving velocities v,  ω/kv = 0, 0.3, 1, 3 and 10.

The distribution Pc(x) is Gaussian with xs= 1 and σs= 0.05, the initial distribution Qini(x) is Gaussian with xini= 0.1 and σini= 0.025.

The described behavior of Fk on T and v qualitatively agrees with the tip-based experiments. Surprisingly, the dependences obtained within the ME approach, perfectly agree with the experimental ones for a "model" tribological system, where the kinetic friction of the driven lattice of quantized magnetic vortexes in high-temperature cuprate superconductors was studied (e.g., compare inset of Fig.11b with Fig.3 of Maeda et.al. Int.J.Mod.Phys. B 19 (2005) 463).

 

Next: Distribution of thresholds

goto main Back to main page or tribology page

Last updated on April 19, 2014 by O.Braun.  Translated from LATEX by TTH