Friction on Mesoscopic Scale

Master equation approach  goto top

 

Earthquakelike model. The EQ model describes the interface between the bottom of the solid block and the fixed substrate. 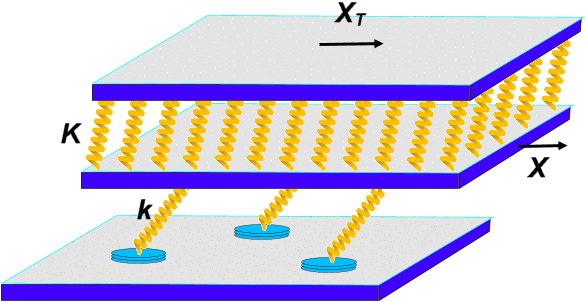It assumes that the interaction occurs through N asperities that make contacts with the substrate. Each asperity is characterized by its contact area Ai  and an elastic constant ki, schematized by an elastic spring, which can be estimated as  ki~ ρc2√Ai,  where ρ is the mass density and c is the transverse sound velocity of the material which forms the asperity. When the bottom of the solid block is moved by X, the stretching xi of an asperity, i.e. its elastic deformation with respect to its relaxed shape, increases. The force at the contact grows as  fi= kixi  until it reaches the threshold value  fsi∝ Ai  at  xsi= fsi /ki∝ √Ai;  at this point the contact rapidly slides, and fi and xi drop to a small value before a contact is formed again.

 

Let  Pc(xs)  be the normalized probability distribution of values of the thresholds xsi at which contacts break. First we consider the model in the quasi-static limit where inertia effects are neglected (this restriction will be removed later, see ). The distribution Pc(x) can be characterized by its average value xs and standard deviation σs;  a typical example is the Gaussian distribution  Pc(x) = G(x; xs,σs) = [1/σ √(2π)] exp[−(x−xs)2/4σ2].

To describe the evolution of the model, we introduce the distribution  Q(x; X)  of the stretchings xi when the bottom of the sliding block is at a position X.  Let all asperities be initially relaxed or weakly stressed, e.g., let the distribution  Q(x; 0) = Qini(x)  be Gaussian,  Qini(x) = G(x; xini,σini)  with  xini= 0  and σini<< σs.  Now, let us adiabatically increase the displacement X of the bottom of the top sliding block while the base (the bottom substrate) remains fixed. The sum of the elastic forces exerted on the bottom of the block by the stretched asperities makes up the friction force

F(X)  =  N ‹ki ›

⌠
 ⌡

∞

-∞

x Q(x; X) dx .

(1)

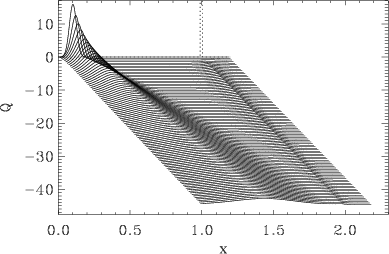
The evolution of the system, deduced from the numerical simulation of the EQ model, is presented in Fig.1. It shows that, in the long term, the initial distribution approaches a stationary distribution Qs(x) and the total force F becomes independent on X.  The final distribution is independent of the initial one (an elegant mathematical proof of this statement was given in Z.Farkas, S.R.Dahmen, D.E.Wolf, J.Stat.Mech.: Theory and Experiment P06015 (2005); cond-mat/0502644; the authors considered a simplified version of the EQ model, assuming that every contact keeps its own threshold value fsi unchanged after breaking/reforming); the statement is valid for any distribution Pc(x) except for the singular case of Pc(x) = δ(x−xs).

Figure 1: (a) Evolution of the EQ model. The curves show the distribution  Q(x; X)  versus x for incrementally increasing values of X with the step ΔX ≈ 1.05. The distribution Pc(x) is Gaussian with xs= 1 and σs= 0.05, the initial distribution Qini(x) is Gaussian with xini= 0 and σini= 0.025 so that F(0) = 0.  (b) Solution of the master equation with the increment ΔX = 1.09  for the same model parameters.  Panels (c) and (d) show the dependences F(X) for  ‹ki› = 1 and  K = ∞  for EQ and ME, correspondingly.

 

Master equation. Rather than studying the evolution of the distribution  Q(x; X)  by simulation of the EQ model, it is possible to describe it analytically. Let us consider a small displacement ΔX > 0 of the bottom of the sliding block (for ΔX < 0 see below). It induces a variation of the stretching xi of the asperities which has the same value ΔX for all asperities. The displacement X leads to three kinds of changes in the distribution  Q(x; X):  first, there is a shift due to the global increase of the stretching of the asperities, second, some contacts break because the stretching exceeds the maximum that they can stand, and third, those broken contacts form again, at a lower stretching, after a slip at the scale of the asperities, which locally reduces the tension within the corresponding asperities. These three contributions can be written as a master equation for Q(x; X):

Q(x; X+ΔX) = Q(x−ΔX; X) − ΔQ−(x; X) + ΔQ+(x; X) .
(2)
The first term in the r.h.s. of Eq.(2) is just the shift. The second term  ΔQ−(x;X)  designates the variation of the distribution due to the breaking of some contacts. It can be written as
ΔQ−(x; X) = P(x) ΔX Q(x; X) ,
(3)
where  P(x)ΔX  is the fraction of contacts that break when the position changes from X to  X+ΔX.  According to the definition of Pc(x),  the total number of unbroken contacts when the stretching of the asperities is equal to x, is given by  N ∫x∞ Pc(ξ) dξ. The contacts that break when X increases by ΔX − so that the stretching of all asperities increases by ΔX − are those which have their thresholds between x and  x + ΔX,  i.e. NPc(x)ΔX.  Thus
P(x)  =  Pc(x) / Jc(x) ,   where   Jc(x)  = ⌠
 ⌡ 		∞

x		 dξ Pc(ξ) .
(4)
The broken contacts relax and have to be added to the distribution around x ~ 0,  leading to the third term in Eq.(2). We denote by R(x) the normalized distribution of stretchings for the relaxed contacts. Writing that all broken contacts described by ΔQ−(x; X)  reappear with the distribution R(x), we get
ΔQ+(x; X)  =  R(x) ⌠
 ⌡ 		∞

-∞		 dξ ΔQ−(ξ; X) .
(5)
Equation (2) can be rewritten as  [ Q(x; X+ΔX) − Q(x; X) ] + [ Q(x; X) − Q(x−ΔX; X) ] = − ΔQ−(x; X) + ΔQ+(x; X).  Taking the limit  ΔX → 0,  we finally get the integro-differential equation – the master equation (ME)
  ∂Q(x; X)
∂x		  +   ∂Q(x; X)
∂X		  +  P(x) Q(x; X)  =  R(x) ⌠
 ⌡ 		∞

-∞		 dξ P(ξ) Q(ξ; X) ,
(6)
which has to be solved with the initial condition Q(x; 0) = Qini(x). Notice that Qini(x) cannot be an arbitrary function, because the contacts that exceed their stability threshold, must be relaxed from the very beginning.

Once the distribution  Q(x; X)  is known, we can calculate the friction force F(X) using Eq.(1). The static friction force corresponds to the maximum of F(X), i.e., Fs= F(Xs), where Xs is a solution of the equation  F'(X) ≡ dF(X)/dX = 0. In order to simplify the further consideration, let us assume that Pc(x) = 0 for x ≤ 0 (this agrees with its physical meaning because, if x < 0, a positive variation ΔX actually reduces the absolute value of the force on a contact, which does not cause its breaking). Also we choose R(x) = δ(x), i.e., we assume that a broken contact sticks again only after a complete relaxation.

Analytical solutions of the master equation can be obtained for some particular cases. Moreover, for one important choice of the initial distribution, when all contacts are relaxed at the beginning, one can find analytically the initial part of the solution in a general case. For the Gaussian distribution of thresholds, a numerical solution of the master equation (6) is presented in Fig.1b. One can see that it is almost identical to that of the EQ model (Fig.1a), except for the noise on the EQ distributions. The distribution  Q(x; X)  always approaches a stationary distribution Qs(x). The final distributions of the EQ model and the master equation approach are compared in Fig.2.

Figure 2: The final distribution Q(x) for the parameters from Fig.1 (solid curve; crosses show the averaged final distribution for the EQ model).

 

The red dotted curve shows the distribution Pc(x), and the blue broken curve shows P(x).

 

The steady-state, or smooth-sliding solution, i.e. the solution of Eq.(6) which does not depend on X, can easily be found. It can be expressed as

Qs(x) = C –1 Θ(x) EP(x),
(7)

where Θ(x) is the Heaviside step function,  EP(x) = e–U(x),  U(x) = ∫0x dξ P(ξ),  and  C = ∫0∞ dx EP(x).  Note also the following useful relationships:  U'(x) = P(x),  EP'(x) = −EP(x)P(x),  Jc(x) = EP(x),  Pc(x) = P(x)EP(x)  for  x > 0, and  EP(x) = 1  for  x ≤ 0.

 

In the general case, let the distribution Pc(x) be of bell-like shape with the maximum at xs and the width σs. When X shifts for the distance xs,  due to the breaking and reforming of contacts with a lower stretching, an initially peaked distribution  Q(x; X)  broadens by the value ~σs (Fig.1). Therefore, any initial distribution tends to the stationary one as  |Q(x; X) − Qs(x)| ∝ exp(−X/X*),  where  X*~ xs2/σs.

Thus, in a general case the solution of the master equation always approaches the smooth-sliding one given by Eq.(7). However, there is one exception from this general scenario: when all contacts are identical, i.e., all contacts are characterized by the same threshold xs, the model admits a periodic solution. This singular periodic solution has been found in simulations of small tribosystems and often analyzed as describing the stick-slip, but actually it is unphysical and ceases to exist as soon as non-equivalent contacts are considered. As will be shown below (see also ), the stick slip can be deduced from the solution of the master equation, but its origin is different. Besides, the ME formalism can be extended to take into account various generalizations of the EQ model as will be described below.

 

Some examples goto top

 

Example 1: Steplike distribution goto top

As a simple example, let us consider the distribution  P(x) = p Θ(x−xs),  or
P(x) = ì
í
î
0       if       x ≤ xs ,
p       if       x > xs .
 
(8)
One can easily find that  C = xs+ p–1,
EP (x) = ì
í
î
1
  for
  0 ≤ x ≤ xs ,
e–p(x–xs)
 for
x > xs ,
 
(9)
Pc (x) = ì
í
î
0
  for
  0 ≤ x ≤ xs ,
pe–p(x–xs)
 for
x > xs ,
 
(10)
F = 1
2		 Nc ‹ki › [ xs + p–1 + p–1/(1+pxs) ].
(11)

In particular, if  xs= 0,  then  Qs(x) = Θ(x)pe–px  and  F = N‹ki›/p,  while for the case of  xs> 0  and  p → ∞  we obtain that  Qs(x) = xs–1  within the interval  0 ≤ x ≤ xs  and  0  outside it, so that  F=1/2N‹ki›xs.

 

Example 2: Rectangular distribution goto top

Figure 3: The stationary distribution Qs(x) (blue dotted line) and the corresponding distribution of static thresholds Pfs(x) (red broken line) for the rectangular distribution Pc(x) (solid line).

 

Remark: the probability distribution Pc(x), which determines the static thresholds {xsi} for newborn contacts, is different from the concrete realization of the distribution of static thresholds Pfs(x), i.e., the histogram calculated over the array {xsi}: while at the beginning Pfs(x) = Pc(x), then the function Pfs(x) evolves with time.

Another simple example which admits the exact solution, is the case of rectangular Pc(x) distribution shown in Fig.3:

Pc(x) =

ì
í
î

0

  if       x ≤ 0.5 ,

1

  if    0.5 < x < 1.5 ,

0

  if       x ≥ 1.5 ,

 

(12)

U(x) =

ì
í
î

0

  if       x ≤ 0.5 ,

−ln (1.5−x)

  if   0.5 < x < 1.5 ,

∞

  if       x ≥ 1.5 ,

 

(13)

EP(x) =

ì
í
î

1

  if       x ≤ 0.5 ,

1.5−x

  if    0.5 < x < 1.5 ,

0

  if       x ≥ 1.5 ,

 

(14)

and the "rate"  P(x)  is given by

P(x) =

ì
í
î

0

  if       x ≤ 0.5 ,

(1.5−x)–1

  if    0.5 < x < 1.5 ,

∞

  if       x ≥ 1.5 .

 

(15)

Example 3: The singular case goto top

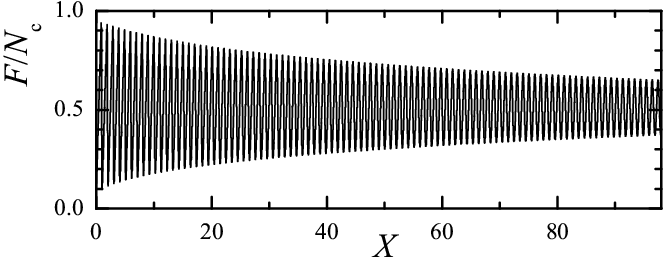
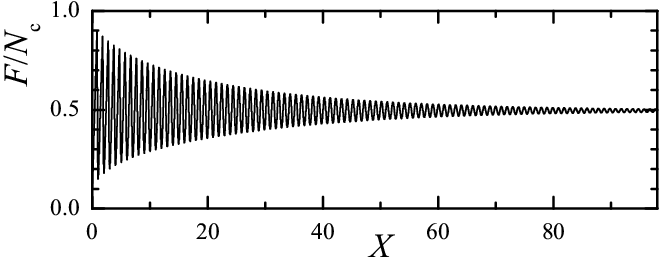
In a general case the solution of master equation always approaches the steady-state solution corresponded to smooth sliding. However, there is one exception from this general scenario, when the model admits a periodic solution and F(X) ≠ const even in the X → ∞ limit.  Namely, this is the singular case when all contacts are identical, i.e., all contacts are characterized by the same static threshold xs, Pc(x) = δ(x−xs), or P(x) = 0 for x < xs and P(x) = ∞ for x ≥ xs. In this case we can find (guess) the steady-state solution of the master equation (e.g., it may be checked by direct substitution):

Q(x; X) = S(x−X) [ Θ(x) − Θ(x−xs) ] ,
(16)
where the function  S(ξ)  is defined by the initial condition:  S(ξ) = Qini(ξ)  for the interval  0 ≤ ξ < xs,  and then  S(ξ)  should be repeated periodically over the whole interval  −∞ ≤ ξ < ∞,
S(ξ ± xs) = S(ξ) .
In this case the total force is equal to
F(X) = Nk [ X + ⌠
 ⌡ 		xs-X

-X		 dξ S(ξ) ] .
(17)

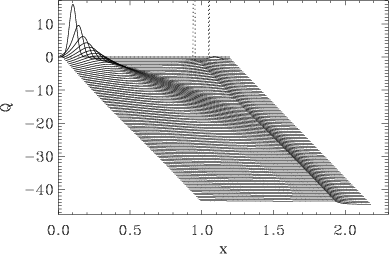
The static friction force takes the minimal value Fs= 1/2Nkxs for the uniform initial distribution Qini(x) = xs–1, when F(X) does not depend on X, and the maximal value Fs= Nkxs for the delta-function initial distribution Qini(x) = δ(x−x0) with some 0 ≤ x0< xs, when the function F(X) has sawtooth shape changing from 0 to Fs.

 

Example 4: Two delta-functions goto top

The periodic solution described above exists only for the distribution Pc(x) with the single threshold. If the contacts are characterized by more than one threshold value, for example, if one part of contacts has the threshold xs1 and another part, the threshold xs2 ≠ xs1  [i.e., Pc(x) is described by a sum of two delta-functions], then the system will always approach the stationary steady state. This is demonstrated in Fig.4, where we compare the system evolution in cases of one-peaked and two-peaked Pc(x) distributions. Notice, however, that this statement is valid only for the infinite set of contacts (the number of contacts with each threshold must be infinite) and cannot be applied for the system where, e.g., two tips move over a surface.

Figure 4: Evolution of the model for two examples of the Pc(x) distribution: Left coulomb is for one-peaked distribution of threshold, Pc(x) = G(x; x1, σ) with x1= 1 and σ = 10–3 (i.e., close to the delta-function distribution), and right coulomb is for two-peaked distribution of threshold,  Pc(x) = 1/2 [G(x; 0.95x1, σ) + G(x; 1.05x1, σ)]  (i.e., close to the distribution with two delta-functions). Solid curves show the distribution Q(x; X)  for incrementally increasing values of X with the increment ΔX ≈ 1,  dotted curves show Pc(x)  (for X = 0 only). The bottom raw shows the corresponding dependences F(X) for ‹ki› = 1 and K = ∞. The initial distribution Qini(x) is Gaussian with xini= 0.1 and σini= 0.025.

 

Example 5: Friction loop goto top

Above we assumed that the slider moves continuously to the right, or ΔX > 0. In the case when the top substrate moves to the left, ΔX < 0, equations (3), (5) and (6) must be modified in the following manner:

ΔQ−(x; X) = −Pb(x) ΔX Q(x; X) ,

(18)

ΔQ+(x; X)  =  Rb(x)

⌠
 ⌡

∞

-∞

dx' ΔQ−(x'; X) ,    and

(19)

 

∂Q(x; X)

∂x

 +  

∂Q(x; X)

∂X

 − Pb(x) Q(x; X)  =  Rb(x)

⌠
 ⌡

∞

-∞

dx' Pb (x') Q(x'; X) ,

(20)

where for the symmetric case (the forward-backward symmetry) we have to put Pb(x) = P(−x) and Rb(x) = R(−x).

The reason for such a behavior is the irreversibility of the master equation. Equation (6) describes the "forward" dynamics when X increases, while Eq.(20) describes the "backward" dynamics when X decreases. Indeed, if the force  fi on a given contact approaches and overcomes  fsi, the contact breaks; but if we now reverse the motion direction, this contact cannot jump back to the value fi ≈ fsi; instead,  fi will decrease until it reaches the value  fi ≈ −fsi .

Figure 5: Friction loop. The distribution Pc(x) is Gaussian with xs= 1  and σs= 0.2,  the initial distribution Qini(x) is Gaussian with xini= 0  and σini= 0.025. The top substrate moves to the right, then to the left, and finally again to the right as indicated by arrows

In a typical tribological experiment, the top substrate moves periodically forward/backward, and in the result, the so-called "friction loop" is obtained. The same loop can easily be calculated with the ME approach as demonstrated in Fig.5.

 

Next: Generalizations of the ME approach

goto main Back to main page or tribology page

Last updated on April 19, 2014 by O.Braun.  Translated from LATEX by TTH