Sliding friction across a thin soft
lubricant film typically occurs by stick-slip, the lubricant fully solidifying
at stick, yielding and flowing at slip. The static friction force per unit area
preceding slip is known from molecular dynamics (MD) simulations to decrease
with increasing contact area. That makes the large-size fate of stick-slip
unclear and unknown; its possible vanishing is important as it would herald
smooth sliding with a dramatic drop of kinetic friction at large size. Here we
formulate a scaling law of the static friction force, which for a soft lubricant
is predicted to decrease as fm+ Δf /Aγ
for increasing contact area A, with γ > 0. Our main finding is that the
value of fm, controlling the survival of
stick-slip at large size, can be evaluated by simulations of comparably small
size. MD simulations of soft lubricant sliding verify the
theory.
Boundary friction of sliding crystal surfaces across atomically thin solid or
nearly solid lubricant layers, of considerable conceptual and practical
importance, also constitutes an open physics problem, because the uncertain
occurrence of stick-slip makes the prediction of the overall frictional regime −
stick-slip or smooth sliding − rather uncertain. While for hard solid
lubricants the answer is known, namely stick-slip for commensurate and
crystallographically aligned interfaces or smooth sliding for lattice
mismatched/misaligned interfaces, it is not so for soft solid lubricants. The
latter, with shearing occuring inside the lubricant rather than at the
surface/lubricant interface, represent the commonest case, realized at room
temperature in e.g. commercial machine oils confined in between metallic
surfaces. The possibility of smooth sliding would be especially relevant,
because of the accompanying large drop of kinetic friction, often a very
desirable outcome. The crucial controlling quantity is the magnitude of static
friction fs − the maximum pulling force
reached before slip. So long as fs is finite
there will be stick-slip; when fs drops to zero,
there can only be smooth sliding. Realistic molecular dynamics (MD) simulations
of lubricants confined between atomically flat surfaces generally indicate that
stick-slip prevails for soft lubricants, with consequently high kinetic
friction. However, while in smooth sliding the kinetic friction per unit area is
essentially size independent, its static counterpart fs
may decrease with increasing contact area A. Despite the increased
computer power, the simulated system sizes are still far too small to establish
conclusively whether in the limit of mesoscopically large size the static
friction will remain finite, and stick-slip will survive with large kinetic
friction, or if it will vanish so that smooth sliding and low dynamic friction
will eventually prevail. The time-honored approach borrowed from equilibrium
statistical mechanics to this type of question is finite-size scaling. One can
for example double repeatedly the size of the simulation cell and compare the
change in the results with some analytically predicted size dependence from
theory. Given a good scaling prediction, a few simulated sizes are often
sufficient to establish the large-size limit with reasonable accuracy, and in
particular whether static friction will drop to zero and stick-slip will
disappear, or not.
Here we solve this question, first by deriving a size scaling law for static
friction, and then showing that it fits realistic MD simulations yielding a well
defined answer. Our end result is that (i) the predicted drop of the
size-dependent part of the static friction per atom fs
is inversely proportional to the linear size of the contact (i.e. to A1/2),
but that (ii) its predicted large-size limit is nonzero, so that
stick-slip will generally survive in soft solid boundary lubrication.
To start off the theory, we inspect first the dynamics of MD simulations of
sliding over soft solid lubricants. These simulations indicate that unlike hard
lubricants where sliding occurs at the interfaces, plastic motion within the
soft lubricant nucleates typically at some weak point well inside the lubricant
film, such as a point defect, a dislocation, a local incommensurability,
etc. (similarly to the "weakest-link hypothesis" of fracture mechanics;
e.g., see
). The
static friction force fs (per substrate atom,
i.e. fs = σsLxLy/Ns,
where σs is the shear stress, Lx
and Ly are the sides of the rectangular simulation
cell, and Ns is the number of substrate surface atoms)
depends on the given initial (frozen) configuration. For a given size A =
Lx×Ly of the simulation cell,
different realizations of the initial configuration will give different
fs values fs1 < fs2
< ..., where a given value fsi is realized
with probability pi(A). Now suppose
we double the simulation cell. Slip-motion will again start at the weakest point
wherever it is, in either half of the doubled cell. Assuming that the new
(larger) contact does not develop new thresholds, the probability that the
doubled cell fails at threshold fsi equals
the sum of the probability that failure occurs precisely at this threshold
fsi in both halfs plus the probability that in
one half the threshold is fsi and in the
other half it is some larger fsj:
| pi(2A)
= ( pi(A) )2
+ 2pi(A) Σj>i pj(A)
. |
|
(1) |
The factor 2 accounts for the the two symmetric realizations of fsj
and fsi in the two halves.
By iteration Eq.(1), we can find the probability pi(ΛA)
for larger and larger cell size ΛA
= 2nA, with n=0,1,...
Given the resulting distribution, one can calculate the average static
threshold for the ΛA cell by
To illustrate this approach, consider the simple instructive example where only
two thresholds fs1= fm and
fs2= fm+ Δf
> fm occur, with probabilities p1 and
p2. For the doubled cell, we have four possible thresholds
realizations: (fs1, fs1) with
probability p12, (fs1,
fs2) with probability p1p2,
(fs2, fs1) with probability
p2p1, and (fs2, fs2)
with probability p22. Accordingly, the doubled cell
fails at the lower threshold with probability p12+
2p1p2, and at the upper threshold with
probability p22. Indicate with p1(A)
= 1 − α and p2(A)
= α < 1. The iteration chain is p2(2ΛA)
= [ p2(ΛA) ]2,
with solution p2(ΛA)
= αΛ, and thus
p1(ΛA) = 1
− αΛ.
Accordingly, the average static friction approaches the minimum threshold
fm exponentially in Λ:
| fs(Λ) −
fm = αΛ Δf = eΛ
lnα Δf
. |
|
(3) |
|
 |
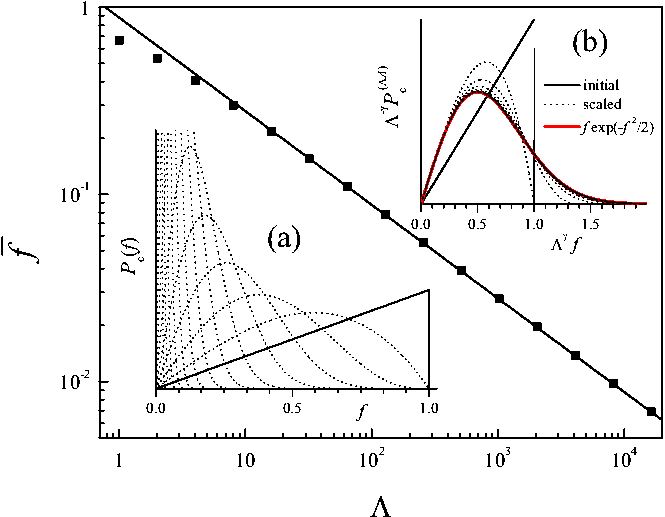Figure 1: Iteration of Eq.(4)
starting from a sawtooth initial distribution Pc(A)(f)
= 2f Θ(f) Θ(1−f),
where Θ(x) is the Heaviside step
function.
Inset (a) shows successive iterations of Pc(ΛA)(f) for Λ = 1,2,4,8,...
Inset (b) displays the
scaled distribution Λ–γPc(ΛA)(Λ–γf)
compared to the infinite-size solution (10).
The main graph shows the
average static friction f excess
(above the minimum fm) as a function of
contact size.
|
When we replace the discrete thresholds fsi
with a more realistic continuous distribution with probability Pc(A)(fs),
the first, quadratic, contribution in Eq.(1) can be neglected, and the iteration
equation takes the form
| Pc(2A)(fs)
= 2Pc(A)(fs)
× |
⌠
⌡ |
∞
fs |
Pc(A)(fs')
dfs' . |
|
(4) |
Figure 1a illustrates an example of the numerical iteration of this equation.
Simulations suggest that for large Λ the distribution
Pc(ΛA)(fs)
tends to approach some universal shape, with little dependency on the small-size
distribution Pc(A)(fs),
once it is rescaled appropriately. A similar scaling behavior was proven for the
strain distributions of the fiber-bundle models, where the
conditions for the emergence of a critical point, i.e. a finite stress in the
large-scale limit, were investigated under the assumption of a nonzero
single-fiber breaking probability for arbitrarily small stress. Here instead we
consider that the minimal contact ("single fiber") distribution
of unpinning forces fs can start off at a minimum
fm which can be nonzero. Iteration of Eq.(4) guarantees
that for any contact size ΛA the distribution
Pc(ΛA)(fs)
vanishes below the same fm as Pc(A)(fs):
scaling preserves fm. To address the scaling of
the distribution above fm, it is convenient to
introduce f = fs− fm.
Let us assume that at large Λ the normalized
probability distribution scales as
| Pc(2ΛA)(f)
= a Pc(ΛA)(a
f) , |
|
(5) |
where a > 1 is a constant. By substituting Eq.(5) into Eq.(4), for the
large-size distribution g(f) = limΛ →
∞ Λ–γPc(ΛA)(Λ–γf),
with γ = log2a, we obtain the
following equation:
| a g(af)
= 2g(f) |
⌠
⌡ |
∞
f |
g(f
') df ', |
|
(6) |
or
| |
a g(af)
g(f) |
= 2 |
⌠
⌡ |
∞
f |
g(f ') df
'. |
|
(7) |
Differentiating both sides with respect to f, we get
| a2g'(af)
g(f) − a g(af) g'(f)
+2g3(f) = 0 . |
|
(8) |
The solutions of this equation depend on a single feature of the distribution
g(f), namely its small-f behavior. More precisely,
assuming that g(f) = Σk=k0ck f k with k0
> −1, we have that
| |
|
|
| a = 2γ
with γ
= (1 + k0)–1
, |
|
|
(9) |
| |
|
|
| ck0
f k0 exp |
[ |
− |
ck0
f 1+k0
1 + k0 |
] |
|
|
|
(10) |
|
solve Eq.(8). Figure 1b demonstrates the approach of the scaled distributions
to the function g(f) = f exp(− f 2/2)
(with a = √2) obtained by starting off with an
initial distribution Pc(A)(f)
= 2 f Θ(f) Θ(1−f),
i.e. with k0=1, c1=2.
The scaling theory makes the following predictions: (i) as scaling
preserves fm, it is possible to predict the
minimum threshold fm from an evaluation of Pc(A)(f)
at the smallest contact size; (ii) the iteration defined by Eq.(4)
preserves the leading term in the f power expansion of Pc(A)(f)
above fm; (iii) regardless of the overall
shape of the small-size threshold distribution, for large size the distribution
acquires the "universal" shape of Eq.(10); (iv) its width
Δf (ΛA)
scales down as an inverse power law of Λ; (v) this
power law is dictated uniquely by the leading power law with which the
arbitrary-size threshold distribution behaves for fs
near fm; (vi) as Λ increases,
the average friction force fs
approaches fm according to the law
| fs(Λ) −
fm ≈
[ fs(Λ=1) −
fm ] Λ–γ. |
|
(11) |
In the example of Fig.1, this relation yields a mean excess static friction
scaling as the inverse square root of size fs−
fm ∝ Λ–1/2.
To validate our prediction with MD
simulations, we use the previously developed
model. Each of the two substrates
is modeled by two atomic layers, one rigid and one deformable. In the minimum
size simulation of contact area A, these substrates are composed by 12×11
atoms arranged in a square lattice. The space between the substrates is filled
by three incomplete layers of lubricant atoms (to prevent crystallization of the
lubricant, we put approximately 90% of the atoms which would complete three perfect monolayers). All atoms interact according to the Lennard-Jones (LJ) potential.
The strength of the lubricant-lubricant interaction is Vll=1/9
(in dimensionless "natural" units, n.u., defined above), while the
lubricant-substrate interaction is much stronger, Vsl=1/3.
The equilibrium distance of the LJ lubricant-lubricant interatomic potential is
rll/as = 3.95/3 (i.e., the
solid lubricant is incommensurate with the substrate). These parameters
correspond to a soft lubricant. Once the thin soft lubricant film is interposed
between the sliders, sliding takes place inside the lubricant (as opposed to
hard lubricants, where the sliding would take place at the interfaces) and the
film melts during sliding, realizing the melting-freezing mechanism of
stick-slip motion. The bottom substrate is kept fixed, while the rigid top
slider layer is pressed with a load of 0.1 n.u. per substrate atom (representing
a pressure in the order 100 MPa if the model represented a noble gas solid
lubricant between metal surfaces) and driven through a spring of elastic
constant k = 3×10–4 n.u. per atom
with a velocity v. We carry out simulations at driving velocities v
= 3×10–3 −
3×10–2 n.u. These velocities are
sufficiently small that the system exhibits stick-slip motion, as illustrated in
Fig.2a. We carry out runs of duration exceeding 107 n.u. for the
smallest-size system (12×11), representing Λ=1. By
extracting the "static friction" thresholds fsi
marked by circles in Fig.2a in correspondence to the peaks in f(t)
preceding each slip event, we obtain a set {fsi}
sampling the probability distribution Pc(A)(fs).
We evaluate this distribution by means of a histogram of 1,063 thresholds
obtained during a long run, and shown in Fig.2b. Although the detailed
behavior near the minimum threshold fm is
naturally affected by limited statistics, the data are consistent with a
distribution staring off at fm≈ 0.0075, with an approximately linear slope (k0=1),
which produces an exponent γ=1/2. From the
threshold distribution Pc(A)(fs)
we extract the mean value fs= 0.0397, marked by a dotted line in Fig.2b.
|
 |
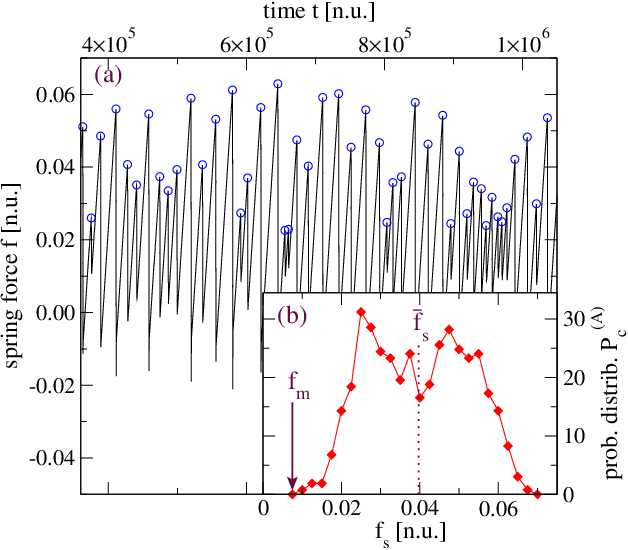Figure 2:
(a) The time evolution of the spring force during a segment of the
simulated stick-slip dynamics of the 12×11 substrate model driven at
speed 0.01 n.u., with an applied load of 0.1 n.u. per rigid substrate
atom; circles mark the stick-to-slip transitions where the individual
static-friction thresholds fsi are
extracted.
(b) The probability distribution of the static-friction thresholds Pc(A)(fs)
as estimated by a histogram of the fsi
values. A dotted line marks the mean value fs,
and an arrow marks the estimated fm.
|
Having thus characterized the small-area sliding behavior, we proceed to
increase the area in order to track the size-induced changes. The cell is
successively increased to Λ = 2=2×1, 3=3×1, 4=2×2,
6=3×2, 9=3×3, 12=4×3, 16=4×4, 20=5×4, and 25=5×5. The results are presented in
Fig.3. As expected, the average static friction decreases with system size. As
was noted, it would not be feasible to extract a large-size limit in the absence
of a scaling law. We find that scaling law (11) with γ=1/2 fits the simulation results with reasonable accuracy. The static friction
tends to a finite large-size value fm > 0, and
therefore stick-slip will survive at macroscopic size.
|
 |
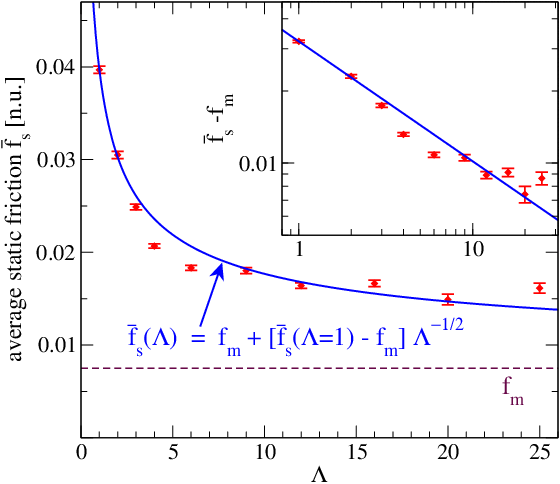Figure 3: The average static
friction force per substrate atom as a function of the system size, as
obtained from molecular dynamics simulations in the same conditions as
those of Fig.2, with several sizes multiple of the 12×11 substrate model
which is represented by the first Λ=1 point
in figure.
The solid line shows the scaling law, Eq.(11).
The dashed line marks fm,
estimated by the lowest observed slip threshold in all simulations of
all sizes.
Inset: log-log scale.
|
We just arrived at the conclusion that once fm
starts off nonzero, fs will converge to
fm> 0 and static friction will not disappear in the
large-size limit. One should however not jump to the conclusion that once the
static friction threshold distribution starts from zero, fm=
0, the amplitude of stick-slip jumps of f(t) will drop to
zero, and stick-slip friction will necessarily disappear in the limit of large
contact area. There are two reasons why this is not generally true. The first
reason resides in statics, and follows from elasticity of the substrate. The
size λc of a domain that can be
considered as rigid and slides as a whole, is determined by the
elastic
correlation length. Therefore, the average static friction force
should reach a plateau for sizes L ~ A1/2
> λc. The second reason follows
from kinetics. When the sliding motion starts at some weak contact site, it
may either die off, or spread over the whole interface with some speed c.
This process takes a finite time τ ~ L/c.
If at a given driving velocity v, τ is of
order or larger then the time between successive slips τss~ fs(L)/(kv),
then the local sliding initiated by this weak contact will lose its role and
effectiveness for all sizes L > λd ,
where λd = (c/v) fs(λd) /k,
hence the static friction will saturate rather than decrease further to
fm as predicted by the scaling theory Eq.(11).
This leads us to ask more generally what is lost in the scaling approach? We
assumed that the doubled cell has the same set of thresholds {fsi}
as the original one. Yet a larger cell may develop new collective excitations,
e.g., a dislocation loop of a size > L. However, if the original cell
A is large enough, we may still safely extrapolate its distribution to a
mesoscopic size, where the master equation approach is applicable.
Another situation where a different behaviour is expected is the Aubry
incommensurate superlubric state, which has zero static friction threshold in
the infinite system. That state, corresponding to fm=
0 in our theory, occurs preferentially for hard lubricants whose interior does
not develop a shear band, and which do not melt during sliding.
Experimentally, the scaling behavior predicted here could be probed by comparing
friction-force microscopy realizations with tips of different curvature radii
sliding on a surface covered by a lubricant close to its melting points, e.g. an
octamethylcyclotetrasiloxan or an ionic liquid at room temperature, or a
noble-gas layer at a cryogenic temperature. The technological bottomline lesson,
finally, is that stick-slip could be attenuated by reducing the smallest
threshold force, for example by promoting extra defects in the lubricant film by
additives or other means.
Published in: O.M. Braun, Nicola Manini, and Erio
Tosatti, Phys. Rev. Lett. 110 (2013) 085503 "Size scaling of static
friction"
Last updated on April 22, 2014 by O.Braun.
Translated from
LATEX by
TTH
Next:
Self-ordering of the lubricant
Back to
main page or
tribology page