As was shown
above, the use of solid
lubricants may be a very promising way, especially in micro-devices, where
conventional lubricants may often be ineffective or may even work like a glue.
In an ideal case of contact of two rigid crystalline incommensurate surfaces the
static frictional force is zero (moreover, the same
is true even for commensurate surfaces if they are not perfectly aligned).
Analogously, if the lubricant film has a crystalline structure and is confined
between two flat substrates with the ideal structure, the friction coefficient
in such perfect-sliding system may be as low as
μ ~ 10–3
to 10–2 or even lower. The critical
velocity of the transition from stick-slip to smooth sliding is also quite
small, vc~10–2c.
Unfortunately, such an ideal system can hardly be reproduced experimentally:
even specially prepared surfaces are not perfectly smooth on a mesoscopic scale,
and a lubricant has typically numerous structural defects. As a result, the
static frictional force fs is large enough, and the
solid lubricant will melt at the onset of sliding. Then, at stick, the film
solidifies back, but, again, either in an amorphous state or in a state with
many defects, because the cooling of the confined film is very rapid due to very
good thermal contact with the substrates. According to
simulation, in such a system one
finds μ > 0.1 and vc~ 0.1c, i.e., the tribological characteristics are even more
worse than those of liquid lubricants. In what follows we will explore whether
the system itself may approach the desired perfect-sliding regime for a suitable
choice of the solid lubricant. Indeed, the energy pumped into the system due to
external driving has to be converted into heat. Therefore, the effective
lubricant temperature T* must increase during sliding.
It is this increase of the temperature that leads to melting of the lubricant in
the melting-freezing mechanism of stick-slip. However, if T*
will remain lower than the melting temperature Tm, the lubricant film could remain solid and, at the same time, its structure may
become more ordered due to annealing of structural defects, especially if T* will be close to Tm. Because
Tm is determined by the interactions within the lubricant, one may play with the
parameters of interaction looking for a situation when Tm
is
close to (but higher than) T*. Below we show that, indeed, a
suitable choice of the parameters may lead to the desired self-ordering of the
lubricant and consequently to the low values of the frictional forces.
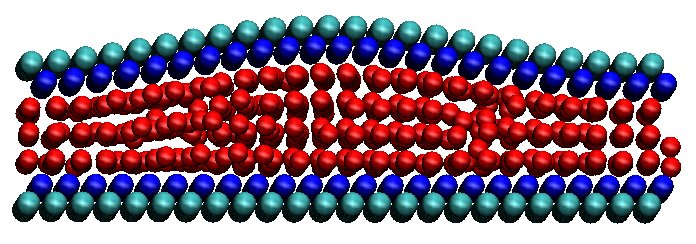
Sliding-induced ordering of the
Nl=1 system for vspring= 0.1
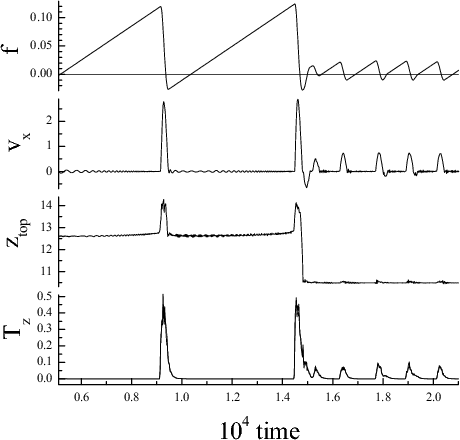 |
|
|
Configuration before
self-ordering |
 |
|
Configuration after
self-ordering |
 |
| |
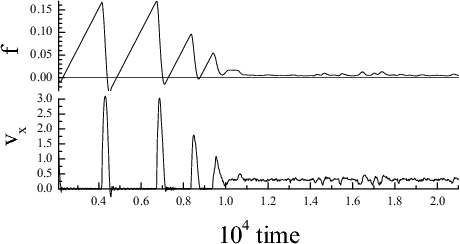
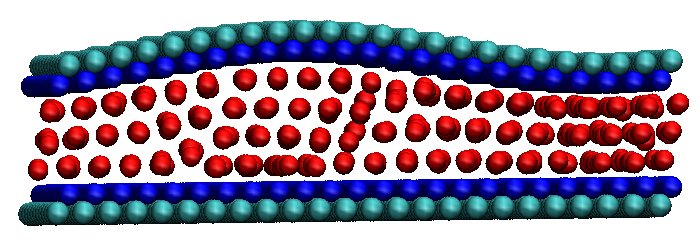
Sliding-induced ordering of the
Nl=3 system for vspring= 0.3 &
movie (avi 1.5 Mb)
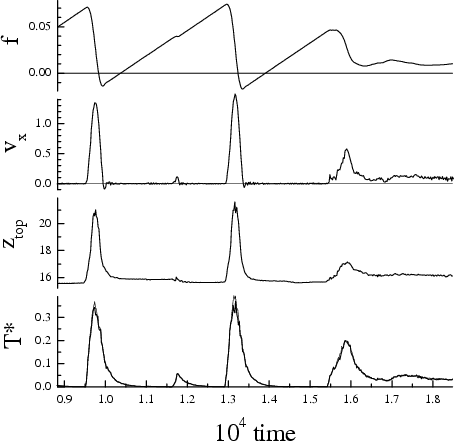
Sliding-induced ordering of the
Nl=3 system with Vll= 0.5 (so that
Vll/Vsl= 1.5) and the curved top substrate
for vspring= 0.1
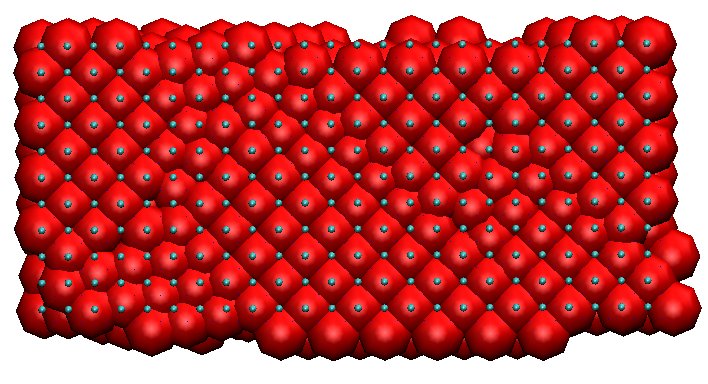
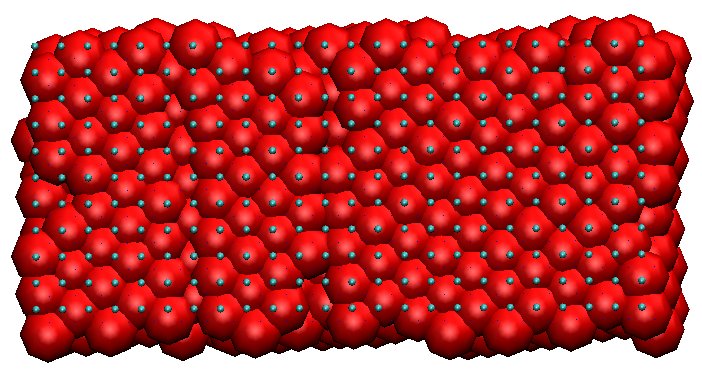
| Configurations: |
| before self-ordering (commensurate) |
after self-ordering (incommensurate) |
 |
 |
 |
 |
| movie
(mpeg 7.2 Mb) |
movie
(mpeg 9 Mb) |
| full
movie (mpeg 15 Mb) |
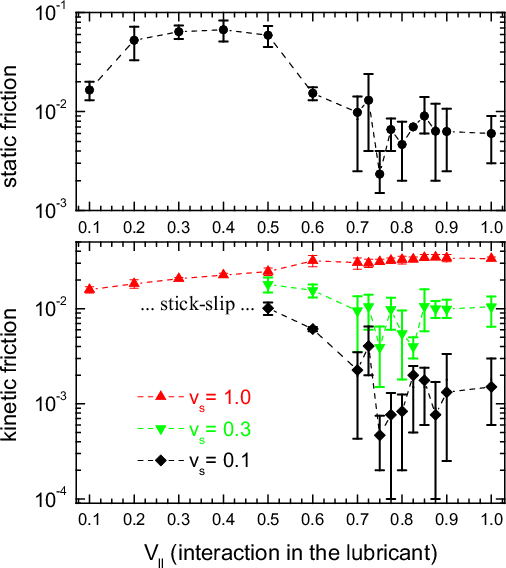
Figure:
Static fs and kinetic fk
frictional forces for three values of the driving velocity (vs=
0.1, 0.3 and 1 as shown in legend) as functions of the interaction amplitude
Vll in semi-logarithmic scale. The error bars
show deviation of the simulation results in different runs.
From this figure we
can observe two clear-cut features: First, as one can judge from the dependence
of fk on vs, the
mechanism of the stick-slip motion changes from the melting-freezing to the
inertia mechanism at Vll ≈
0.5, i.e., for Vll/Vsl ≈
1.5. Most importantly, we observe that for Vll≈ 0.8
the kinetic frictional force fk
achieves a minimum as low as fk ≈ 10–4
to 10–3. The friction coefficient in
this case takes values of order μ < 10–2
which are more than one order of magnitude lower than those attainable with
conventional liquid lubricants. Namely, for the optimum value of
the interaction,
Vll= 0.75, at v = 0.03 we get
smooth sliding with fkinetic≈ 10–4,
so that
µ ≈10–3 (see
movie mpeg 3.3 Mb).
Conclusion
It exists an optimal choice of the
strength of interatomic interaction Vll within the
lubricant, that leads to the minimization of the kinetic friction as well as to
the low critical velocity of the stick-slip to smooth-sliding transition. The
optimal value of Vll should be high enough (relatively
to the amplitude Vsl of the interaction of
lubricant atoms with the substrates) so that the lubricant remains in the solid
state during sliding. At the same time, the value of Vll
should be not too high, in order to allow annealing of the structural defects in
the lubricant. For the parameters used in the simulations, the optimum was
achieved at Vll ≈ 2.5Vsl.
Last updated on April 1, 2004 by O.Braun. Translated from
LATEX by
TTH









