As was shown above, the lowest friction is achieved for the hard lubricant film, when the film is solid and crystalline but incommensurate with the substrate surface. In this case, the shape of lubricant molecules is not too relevant, because friction is determined uniquely by the substrate/lubricant interface structure. Conventional lubricants, however, belong typically to the opposite soft lubricant type, with Vll< Vsl. In this case each substrate is covered by a glued lubricant monolayer, protecting it from wear. Sliding occurs deeper inside the lubricant film, where below the film melting point a typical melting-freezing mechanism operates: the lubricant locally melts at slip (during sliding) and resolidifies at stick. For a thick lubricant film above its melting point, friction is proportional to the bulk viscosity of the lubricant. Therefore, thick fluid lubricants consisting of simple spherical molecules or individual atoms, characterized by a low bulk viscosity, would provide the best frictional properties. However, it is well known that long molecules characterized by a high viscosity often make better lubricants. The reason for this is the squeezout effect: at high load, when the regime of boundary lubrication is approached and the film is locally extremely thin, at stick the lubricant may be squeezed out in correspondence of the substrate asperities. Direct contact of unlubricated asperities leads to a high static friction force fs and generally to substrate wear. Sivebaek et al. (I.M. Sivebaek, V.N. Samoilov, and B.N.J. Persson, J. Chem. Phys. 119 (2003) 2314) showed that longer lubricant molecules are harder to squeeze out, and this is why they provide better lubrication properties. Following that line, Sivebaek et al. studied the "totally-glued" case, where all atoms of the lubricant molecule interact strongly with the substrates. Longer molecules adhere more to the substrates, making it harder for the squeeze-out of the last lubricant layer to nucleate. Therefore, longer alkanes perform better as boundary lubricants than shorter ones, because they prevent more effectively the appearance of cold-welded junctions and the resulting wear.
The aim of our work was to study the role of molecular length in detail for a wide range of model parameters. Moreover, we compare a totally-glued lubricant (with all monomers of the lubricant chain sticking to the substrates) to a "head-glued", with a single (head) atom of the molecule strongly attached to the substrate, while the other atoms (molecular tail) interact more weakly with the substrates. Our aim is to clarify the role of the length of the lubricant molecules in friction, in particular to find what length of lubricant molecules could provide best tribological characteristics for a thin (few molecular layers) soft lubricant film. We use the following criteria to define good tribological properties: (i) a better lubricant provides lower values for both the static friction force fs and the kinetic friction force fk, and (ii) a better lubricant is characterized by lower values for the critical velocity vc of the transition from stick-slip to smooth sliding (or at least to provide a less irregular motion in the stick-slip regime).
We choose to explore a simplified two-dimensional (2D) minimal model which is sufficient to catch the physics of the problem, with qualitatively correct trends. Due to model simplicity, we are able to span a large choice of structures and parameters. On top of that, the 2D geometry provides an easier visualization of all processes inside the lubricant. (However, we must note that the 2D model does not describe realistically the lubricant squeezout, which requires a full 3D modeling.)
Thus, we use the model, where point particles, representing individual atoms or monomer units of larger molecules, can move in two dimensions x and z, where x is the sliding direction and z is perpendicular to the substrates. The substrates are modeled as two rigid chains of Ns atoms and lattice spacing Rs, so that the system size in the sliding direction is Lx= NsRs. We apply periodic boundary condition along the x direction. The bottom substrate is fixed at x=z=0, while the top one is free to move in both x and z directions. The top substrate is pressed toward the bottom one by a (-z)-directed constant load force Fl= Nsfl, and is driven in the x direction at velocity vs through an attached spring of elastic constant Nsks, as sketched in Fig.1. The spring force F, which works against the friction force, is monitored during simulation (throughout the paper we report the force per substrate atom f = F/Ns). Thus, our model is a 2D variant of a typical experimental setup used in tribology.
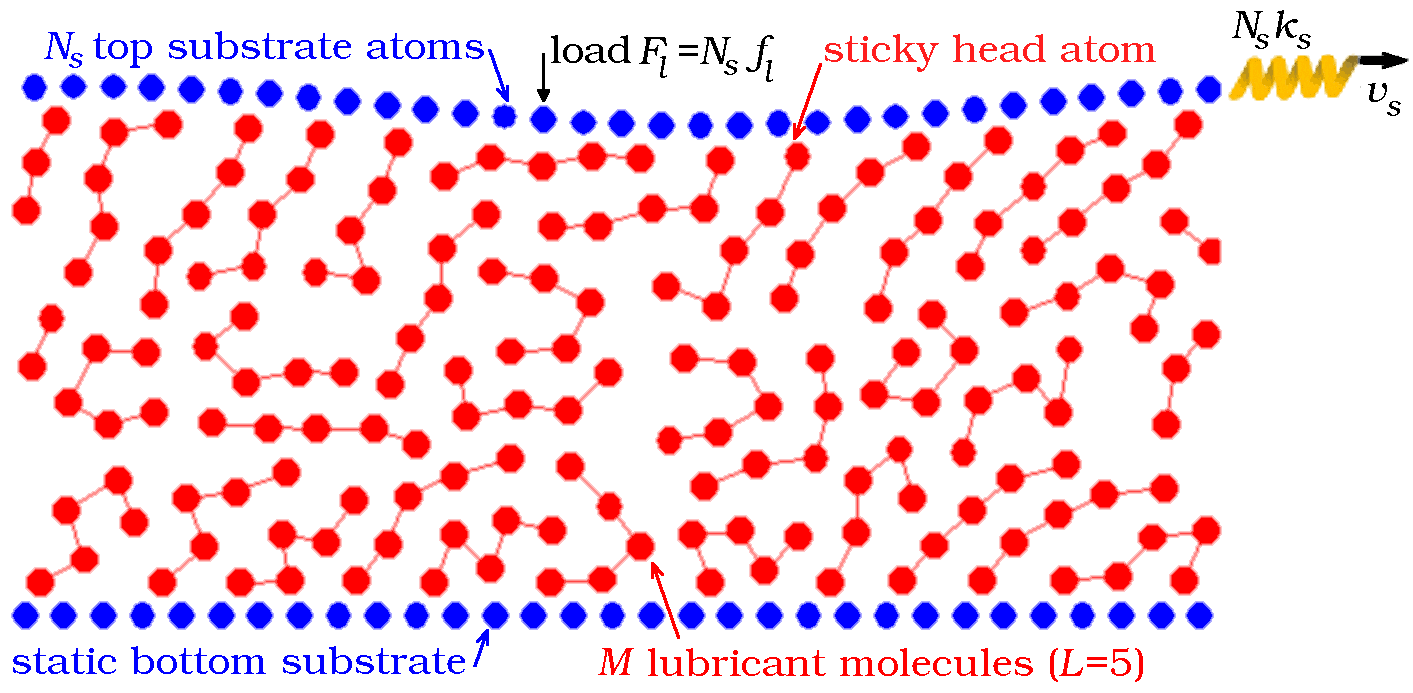 |
Figure 1: A schematic cartoon of the model. This snapshot refers to a configuration where the Ns=31-atoms substrates (blue) squeeze M=35 head-glued molecules, each made of L=5 atoms (red) |
|
(1) |
|
(3) |
where we typically use η0= 1 and zd≈ 1. This form is meant to mimic the Joule heat dissipation, which can only take place through the substrates, and therefore is mostly effective at the interfaces.
We compare the main tribological properties of lubricants consisting of molecules of different lengths, from individual (atom-like) monomers to linear chain molecules composed of L atomic/monomeric units, so that the number of lubricant molecules is M=N/L. To build chain molecules, we follow the Muser-Robbins procedure (M.H. Muser and M.O. Robbins, Phys. Rev. B 61 (2000) 2335). The lubricant is described with the Kremer-Grest bead-spring model (K. Kremer and G.S. Grest, J. Chem. Phys. 92 (1990) 5057), which yields realistic dynamics for polymer melts (W. Tschöp et al., Acta Polym. 49 (1998) 61). While all monomers within a molecule still interact with each other via the LJ potential, Eq.(1), adjacent monomers inside a given molecule (chain) interact via an additional ("FENE") potential
|
(4) |
where RCH= 1.336Rll and VCH= 33.75Vll. This additional potential has the main effect of preventing molecular breaking. Besides that, it is fairly small at the equilibrium distance r = Rll of VLJ, and causes a bond-length contraction to Rmol≈ 0.856Rll.
In the simulations, each substrate contains Ns=62 atoms and the substrate lattice constant is chosen as Rs=2/3, moderately "incommensurate" with the lubricant equilibrium interatomic distance Rll=1, a feature not atypical for lubricant/substrate interfaces. Accordingly, the system size is Lx= 41.3. This fits up to N=50 atoms (in the atomic lubricant case) in one monolayer film under a standard applied load fl=1. The N=100 atoms therefore complete two monolayers (one glued to the bottom substrate, the other to the top substrate). Atoms in excess of 100 pile up in between, giving rise to a third, then fourth, etc., layer.
To guarantee an efficient melting-freezing of the soft lubricant in correspondence to the stick-slip motion for the "incommensurate" lubricant-substrate interface, we require a rather strong inequality Vsl >> Vll. Specifically, we choose Vll = 1/9 and Vsl = 5. In detail, we set the lubricant-substrate interaction energies to be Vsl = 5 in the "totally-glued" case, while for the "head-glued" system, the large interaction Vsl = 5 applies exclusively to the "head" molecular atom, while other atoms in the rest of the molecule (the "tail") interact with the substrates with the much weaker Vsl' = 1/9. With these parameters, the melting temperature of the lubricant is of the order of T ~ 0.1; it is a generally decreasing function of the lubricant layer thickness, but an increasing function of the chain length and applied load.
The load force used is typically fl=1 per substrate atom. Assuming an energy scale 9Vll ≈ 0.1 eV and interatomic distances Rll ≈ 0.3 nm (typical of Van-der-Waals intermolecular interactions), in a hypothetical 3D
geometry such load would correspond to a pressure of almost 1 GPa. The top
substrate is driven at an average velocity vs through a
relatively stiff spring of elastic constant ks= 0.1. For
the remaining parameters, we take Rsl = Rs
and zd = Rs. We run all
simulations starting from well-relaxed and annealed initial configurations, and
exclude from averaging any initial transient leading to the steady dynamical
state. In more detail, we solve the Langevin equations of motion using a
fourth-order Runge-Kutta method with a time step Δt = τ0/128, where τ0= 2πRll
(72·9 Vll/ml)
As in typical tribological systems, we observe a transition from stick-slip to smooth sliding with increasing driving velocity. An example is shown in Fig.2. In the smooth sliding regime, the kinetic friction force can easily be measured as the average of the spring force f(t). To evaluate the static friction force fs in the stick-slip regime, one can calculate the histogram P(f) of f(t) and then select fs as the point where P(f) decays below a given level, e.g., P(fs) = 0.5 maxP(f) (see Fig.2c). A harder problem is that of determining the precise transition from stick-slip to smooth sliding and its critical velocity vc, since this transition is often a smooth crossover. For this purpose, we calculate the distribution (histogram) P(ξ) of an auxiliary variable ξ, defined as ξ(t) = [df(t)/dt]/(ksvs). In smooth sliding the function P(ξ) decays monotonically from a maximum at ξ ≈ 0 (see Fig.2f). In contrast, for stick-slip, P(ξ) should show a maximum at some 0 < ξ ~ 1 (Fig.2e). Indeed, during sticks the force grows as f(t) ≈ ksvst [so that P(ξ) = δ(ξ−1)], and it drops quickly to substantially smaller values during short slip events. Thus, this method allows us to evaluate vc fairly accurately.
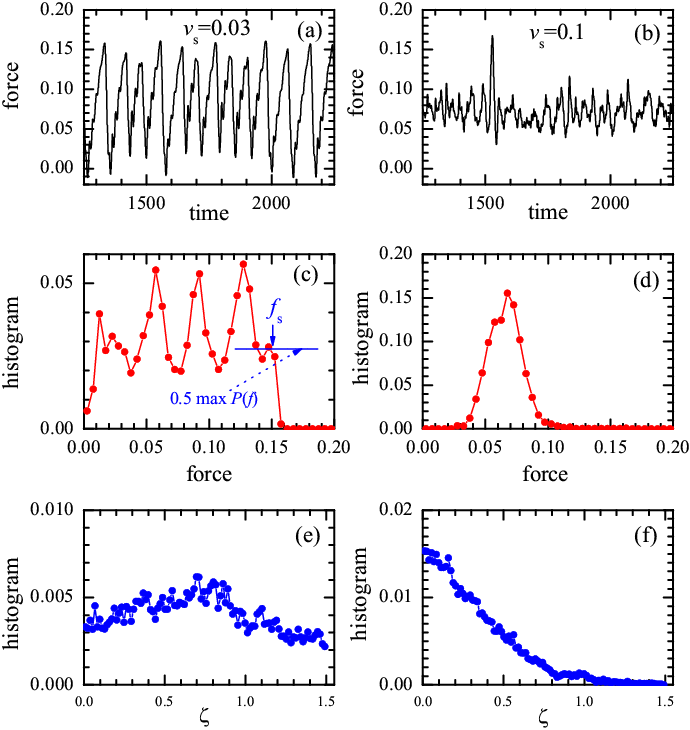 |
Figure 2: Comparison of the stick-slip motion [vs= 0.03,
panels (a,c,e)] and the smooth sliding [vs= 0.1,
panels (b,d,f)] for M=40 totally-glued three-atomic (L=3)
lubricant molecules at T=0.
Panels (a) and (b): typical time dependence of the friction force f(t); panels (c) and (d): histogram P(f) of the friction force f(t); panels (e) and (f): depth distribution P(ξ). The top substrate is curved (see Fig.1), and the parameters are the following: Vll=1/9 and Rll=1, Vsl=5 and Rsl=Rs, fl=1, ks=0.1, Rs=2/3, and Ns=62
|
Typical movies for L=5, vs=1, Δt=0.25 (the top substrate is curved, Vll=1/9 and Rll=1, Vsl=5 or 1/9 and Rsl=Rs=2/3, fl=1, ks=0.1, and Ns=62):
 |
totally glued |
|
|
head-glued |
For the chosen set of parameters, the transition from stick-slip to smooth sliding occurs at a velocity vs<1; therefore, we select vs=1 to represent the smooth-sliding regime, where we calculate the kinetic friction force. Figure 3 summarizes the simulation results for T=0, reporting the time-averaged kinetic friction force fk as a function of the total number of lubricant atoms, which is basically proportional to the lubricant layer thickness, for different molecular lengths L.
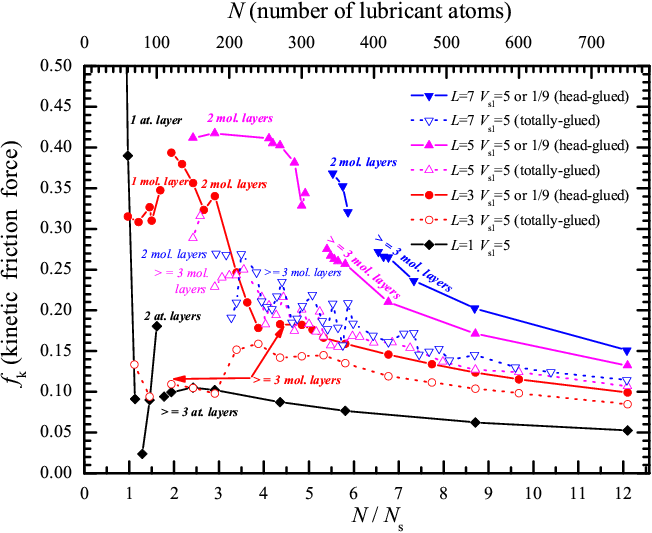 |
Figure 3: Smooth sliding (T=0, vs=1) time-averaged kinetic friction force fk as a
function of dimensionless coverage N/Ns
(bottom scale), as well as total number of atoms N=ML (top
scale) for linear lubricant molecules of different lengths L=1
(black diamonds), 3 (red circles), 5 (magenta up triangles), and 7 (blue
down triangles), for either the totally- (open symbols and dotted lines)
or head-glued (solid symbols and curves) cases.
The top substrate is curved, and the other parameters are the following: Vll=1/9 and Rll=1, Vsl=5 or 1/9 and Rsl=Rs, fl=1, ks=0.1, Rs=2/3, and Ns=62 |
The monoatomic lubricant (diamonds in Fig.3) forms two complete monolayers for N=100 and three monolayers for N=150. For N≥150, one ordered layer sticks to the bottom substrate and another ordered monolayer to the top substrate, while the layer(s) in between are liquid during sliding. For the monatomic lubricant, the static friction force (not shown) is larger than the kinetic friction by a factor of 2 to 4; the transition from stick-slip to smooth sliding occurs at vc > 0.03. Friction generally decreases as the number of lubricant atoms N (and thus the lubricant thickness) grows, but the dependence fk(N) cannot be described by the simple laws of viscous-friction flow. At lower lubricant thickness 100 < N < 150, when the middle layer is incomplete, friction is slightly lower than for three complete monolayers, see Fig.3. When the lubricant amount decreases further, 70 < N ≤ 100, there remain only two, generally incomplete, lubricant layers, each glued to the nearest substrate (e.g., N=100 atoms form exactly two complete lubricant layers, which slide slowly, thanks to incommensurability, over the substrates to which they are attached). At even smaller values of N we have one monolayer or eventually just a monolayer island in the narrow gap between substrates, and at this point both the friction and the critical velocity vc grow rapidly when N decreases.
For all chain molecules (polymer
lubricant) L>1, friction is always larger than for the monomer
lubricant. The kinetic friction force increases with the chain length L,
if the total number of atoms N is kept fixed. In general, regardless of
L, friction decreases roughly monotonically with increasing N, the
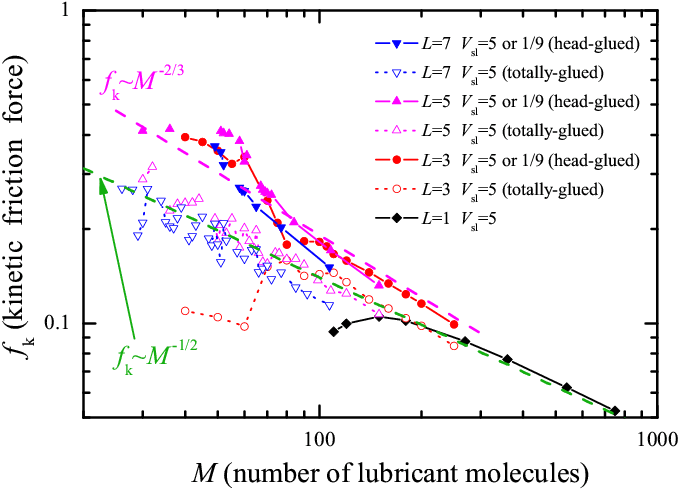
lubricant thickness. In Fig.4 we re-organize the kinetic friction fk
data of Fig.3, but as a function of the number of molecules M (only
points corresponding to three or more molecular layers are shown). In the
standard viscous flow of a fluid with a viscosity η,
the friction force fk should depend on the thickness
d=‹Z› of the
liquid layer (d ∝ N ∝ M) as fk=ηvsRs2/d. Unlike expectations for a fluid lubricant at high temperature, at T=0 the
log-log plot of the function fk(M) suggests that
the simulation data may be (crudely) fit by power laws fk ≈ 0.18 (M/Ns)
 |
 |
|
Figure 4: Smooth sliding: kinetic friction force fk a s a function of the number of lubricant molecules M (of different lengths L) in a log-log scale. Parameters and notation are as in Fig.3. Dashed lines describe power-law fits. |
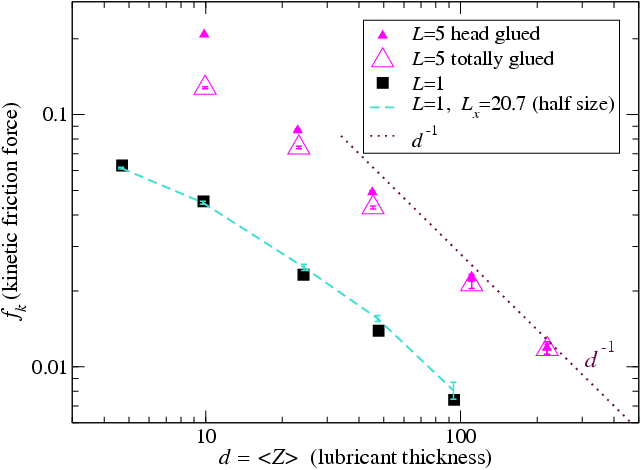
Figure 5: Kinetic friction force fk as a
function of the lubricant thickness d=‹Z›
(roughly proportional to N) in log-log scale. The parameters and
notation are as in Fig.3, except for T=0.2. The dotted line
sketches the fk ∝ d |
Figure 5 reports similar calculations
carried out at a finite temperature T=0.2, compared to which the extra
kinetic energy induced by shearing at sliding velocity vs=1
becomes negligible when the lubricant thickness exceeds about 100Rll. When the lubricant thickness exceeds such values we do observe a crossover to
the expected scaling fk ∝ (M/Ns)
Analyzing the simulation movies for the totally-glued lubricant with L>1 and large enough N we observe two complete layers sticking to the corresponding substrates and a liquid lubricant between these layers. However, not all boundary molecules are glued completely, some of them are glued partially, i.e., only a part of a molecule sticks to the substrate while another part is detached and points into the lubricant bulk. It is precisely these "free tails" that make the friction higher as compared with the monoatomic case. At lower lubricant thickness (M ~ 50 for the L=3 case, M ~ 35 for the L=5 case, and M ~ 25 for the L=7 system) the middle layer is incomplete: its molecules group together at the narrowest intersubstrate gap and just ahead of it (jamming/plowing effect). With a further decrease of lubricant thickness, sliding takes place at a single interface only, namely between the lubricant layers which are attached to bottom and top substrates. In this case, we observe a slow "caterpillar" motion of glued molecules relative the substrate, but this effect is weak because of the strong lubricant-substrate interaction. At even lower lubricant thickness occasional molecules may be glued to both surfaces simultaneously, and in such cases the molecular end sticking with fewer atoms slides along the corresponding substrate.
Next, let us analyze the head-glued lubricant, comparing its behavior to the totally-glued one described above, all other parameters being the same. Firstly, the head-glued system (solid symbols in Fig.3) display a systematically higher friction than the totally-glued lubricant (open symbols). As in the totally glued case, the surfaces are covered by lubricant layers. The layers are orientationally ordered: the molecular heads are attached to the corresponding surface, while the tails are directed outside the surface, and inclined in the sliding direction, like combed hair. Also, the sliding interface is more "irregular", than in the totally-glued system. Therefore, one may expect a smoother frictional motion even in the stick-slip regime at low driving velocities. It is important to note that contrary to the totally glued case, in the head-glued system we find essentially no jamming effects even at low lubricant thickness.
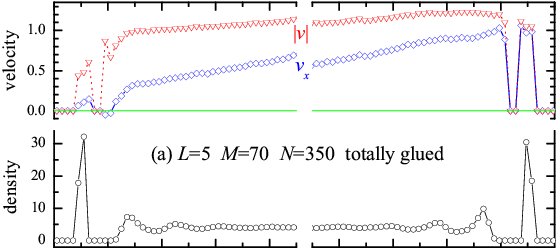
Figure 6 depicts the different atomic density ρ(z) and velocity distributions vx(z) and |v(z)| across the lubricant for the totally- and head-glued molecular lubricants. In both cases, one layer sticks to the substrate, but the thickness of this layer is ~Rll in the totally-glued system and much thicker, <LRmol, similar to the molecular gyration radius, in the head-glued case. Accordingly, while the sliding profile vx(z) is fairly linear in the totally-glued case, in the head-glued case the shearing dissipation concentrates mostly in a bulk lubricant region remote from the substrates.
|
 |
|
Figure 6: z-distribution of the average density (circles) and atomic velocities for (a) the totally-glued molecules (open symbols) and (b) the head-glued (solid symbols) system with L=5 and M=70 (N=350; other parameters as in Fig.3). Triangles stand for the total velocity |v|, diamonds for the x-component of the velocity. |
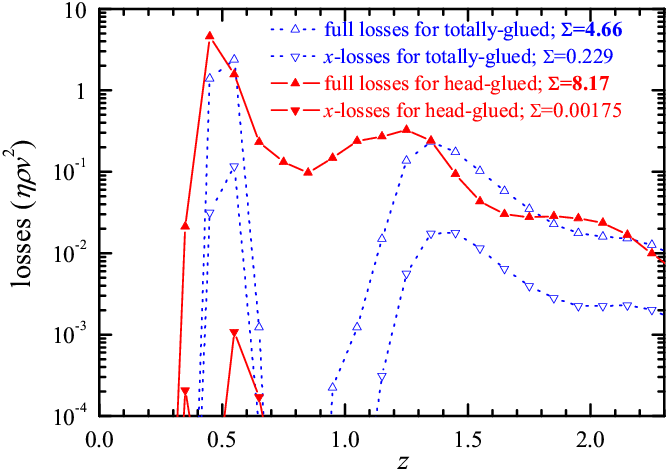
Figure 7: z-distribution of the total energy losses η(z)ρ(z)v2(z) (up triangles) and the x-losses η(z)ρ(z)vx2(z) (down triangles) for the totally-glued (blue open triangles) and head-glued (red solid triangles) lubricants for the model parameters as in Fig.6. The z-integrated energy loss Σ is indicated for each curve. |
To elucidate the different tribological properties of the two kinds of molecular lubricants, in Fig.7 we analyze the distribution of energy losses (dissipated power) due to sliding. The losses occur mainly within the first (glued) lubricant layer. Importantly, we find that the main losses come from atomic vibrations in the transverse z direction, by far dominant over those coming from the motion along the driving x direction. This observation explains why, even though head-glued molecules displace sliding away from the substrates surfaces where most dissipation takes place, the head-glued system leads to a higher friction: transverse vibrations of larger amplitude penetrate better near the substrates (where most dissipation occurs) through head-glued molecules than through totally-glued ones.
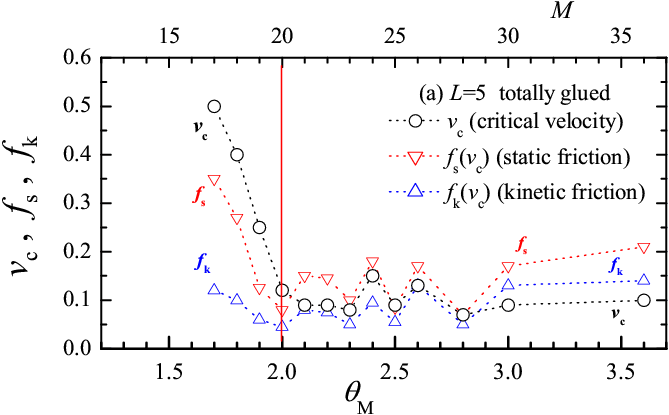
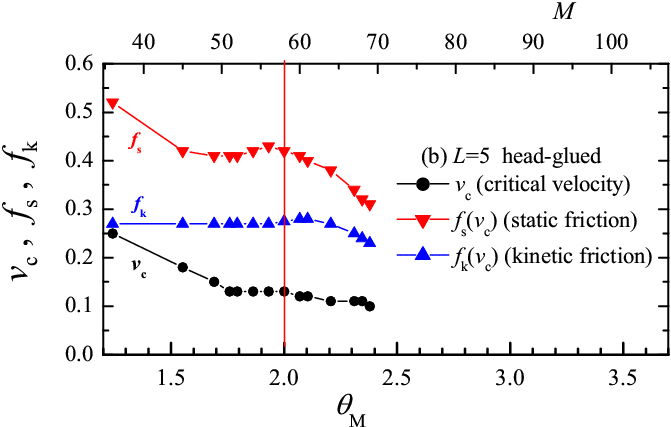
Our results suggest that a totally-glued lubricant is more effective than a head-glued one, because it provides lower kinetic friction. Totally-glued molecules with their stronger sticking to the substrate, should also be more stable against squeezout of the contact area at high load. Unfortunately, in our simplified 2D model we cannot study quantitatively the squeezout process. We can, however, analyze in detail the dependence of frictional forces on the number of lubricant molecules M. Results for the L=5 lubricant molecules are presented in Fig.8. It is useful to define the maximum number of molecules M2 which can arrange themselves exactly to form the two molecular layers (one attached to the bottom substrate and the other to the top substrate), so that sliding takes place in the remaining lubricant just in between these two layers. For the totally-glued lubricant M2≈ 2Lx/[Rll+(L−1)Rmol], and for the head-glued lubricant M2< 2Lx/Rll. M2 depends on L and on the load force, so that it takes an analysis of the MD trajectories to define its precise values. In the current model (with Lx= 41.3, Ns= 62, L=5) we find M2=20 for the totally-glued system and M2=58 for the head-glued case. Based on the definition of M2 we can introduce the dimensionless coverage ΘM = 2M/M2, so that ΘM = 2 corresponds to precisely two molecular layers. Figure 8 shows that, as expected, both the friction force and the critical velocity vc increase when the coverage decreases below the two-layer value. The rise of friction below M2=2 is fairly slow in the head-glued system, but is very sharp in the totally-glued case. In a real 3D system the lubricant is squeezed out from the contact areas at the asperities, where about 2−3 lubricant boundary layers are left, harder to remove. When however the squeezing force is pushed further leaving less than two layers, the head-glued lubricant continues to operate fairly efficiently, while the totally-glued lubricant quickly loses its tribological properties. A similar behavior occurs for chains of length L=3 and 7.
 |
 |
|
Figure 8: Dependence of the critical transition velocity vc (circles) between stick-slip and smooth sliding, of the static friction force (red down triangles) and kinetic friction force (blue up triangles) at the crossover velocity vs=vc upon the dimensionless coverage ΘM (bottom scale), or the number of lubricant molecules M (top scale) for the L=5 chain molecules, for (a) totally-glued and (b) head-glued molecules. Simulation parameters same as in Fig.3. |
|
The described above behavior is illustrated by the following movies:
 |
totally glued; exactly two layers (M=20): smooth sliding |
 |
totally glued; 10% less than two layers (M=18): stick-slip |
 |
head-glued; exactly two layers (M=58): smooth sliding
|
 |
head-glued;
22%
less than two layers (M=45): smooth ("carpet") motion
|
The L-dependence of friction forces is illustrated in Fig.9 for a configuration with exactly two molecular layers (ΘM=2). In detail, the critical velocity vc marks the crossover illustrated in Fig.2, and the frictional forces fs and fk are evaluated immediately below and above vc, in the stick-slip motion and smooth sliding regimes respectively. Note that for the head-glued lubricant, the critical velocity depends only weakly on the molecular length L, while in the totally-glued case, vc increases rapidly with L, so that for long molecules, L>5, the critical velocity of the totally-glued chains is much higher than for the head-glued ones. Note also that the static friction fs for the stick-slip motion at vs< vc is approximately twice as large as the kinetic friction fk in the smooth-sliding regime at vs > vc.
 |
 |
|
Figure 9: Dependence of the static (red down triangles) and kinetic (blue up triangles) friction forces at vs≈ vc and of the critical velocity vc (circles) on the length L of lubricant chains for the coverage ΘM of two molecular layers, in the cases of (a) the totally-glued and (b) the head-glued system. Other parameters same as in Fig.3. |
|
Also we studied the dependence of friction on the temperature T (see Fig.10 for the fixed driving velocity vs= 0.316, smooth sliding), on the load force fl (see Fig.11 for M=70 and L=5), and on the driving velocity vs (see Fig.12 for L=1 (M=N=360), L=3 (M=120 and N=360), L=5 (M=70 and N=350), and L=7 (M=51 and N=357), all for T = 0.1).
Figure 13 demonstrates the dependence of the kinetic friction on the strength of the interaction Vll between the lubricant molecules. At small Vll, e.g., for Vll= 0.1, the surfaces are covered by monolayers of lubricant molecules, and the sliding interface lies somewhere near the middle of the lubricant film. As Vll increases, sliding becomes more and more viscous, thus friction increases reaching a maximum near Vll=Vll*~ Vsl=5. At this point, the sliding mechanism changes: the lubricant becomes rigid enough to move as a whole body, and frictional sliding is now shifted to the substrate/lubricant interfaces. If Vll increases further beyond this point, sliding becomes easier and easier because of increasing lubricant rigidity; this regime corresponds to the sliding of two hard incommensurate surfaces. We found the same type of crossover for other numbers of lubricant molecules.
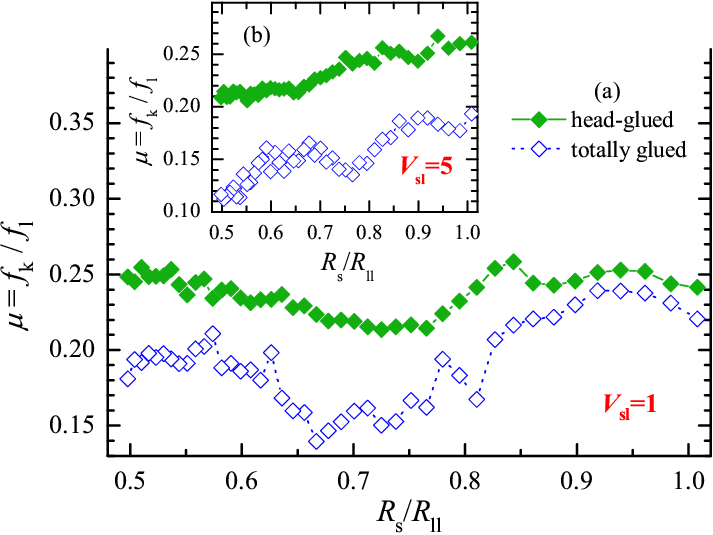
Next, Fig.14 demonstrates the variation of the friction coefficient with the substrate lattice constant Rs. In these simulations, we keep the size of the system constant at Lx= 62×2/3 ≈ 41.3, and vary the number of substrate atoms from Ns= 41 to 83, so that Rs= Lx/Ns changes from ≈0.5 to ≈1. The total load force Fl= flNs is also kept constant at the level Fl= 62 (so that we have fl=1 for Ns= 62 as in the previous simulations). As expected, there appears to be no systematic dependence of friction on the substrate/lubricant interface Rs/Rll for the head-glued system, where the molecules arrange themselves at frequently varying mutual distance, and no commensurability effect can arise.
 |
 |
|
Figure 13: Kinetic friction force fk as a function of the energy amplitude Vll of interaction between the lubricant atoms, for linear lubricant molecules of different lengths L=1 (M=N=360, black), L=3 (M=120 and N=360, red), L=5 (M=70 and N=350, magenta), and L=7 (M=51 and N=357, blue), for either totally- (open symbols) or head-glued (solid symbols) cases. T=0.1, vs=0.1; other parameters same as in Fig.3. |
Figure 14: Friction coefficient μ = fk/fl as a function of the substrate lattice constant Rs for M=70 linear lubricant molecules of length L=5 for totally glued (blue open symbols) and head-glued (green solid symbols) chains. The sliding velocity is vs= 0.316, the interaction radius Rsl=Rs is varied, and in (b) all other parameters are as in Fig.3 including Vsl=5 or 1/9, while in (a) the gluing interaction is Vsl=1 or 1/9. |
For the totally glued case, however, the friction coefficient shows a well pronounced minimum at Rs~ 0.75, especially for a lower value of the lubricant-substrate interaction Vsl=1. This is associated to a slow "caterpillar" motion of the glued molecules in the periodic substrate potential, caused by advancing of kinks (misfit dislocations) at the lubricant-substrate interfaces. For a rigid linear molecule in a sinusoidal potential, virtually free sliding of the molecule should be observed for ratios Rs/Rmol= L/(2L−n), where n=1,2,...,L/2. This gives, e.g., Rs/Rmol= 2/3, or Rs≈ 0.57 for L=2 and 4, and Rs/Rmol= 5/8, or Rs≈ 0.535 for L=5 (for a nonrigid molecule, these values are shifted upwards). As shown in Fig.15, a caterpillar-type motion indeed takes place. However, as some molecules are attached with all L atoms but others stick only partially, e.g., with 2−4 atoms, while the glued layer should move as a whole (the molecules cannot overtake one another), caterpillar motion is disturbed, and this makes the minimum in Fig.14 broad and shallow.
 |
Figure 15: The central region of five successive snapshots of the motion of M=70 totally-glued L=5 lubricant molecules. The time interval between successive snapshots (a) to (e) is Δt=1. Snapshots b-e display only the atoms nearest to the bottom substrate, for better visibility of the caterpillar motion. To provide a clearer reference frame, one of the static atoms in the bottom-substrate is drawn as empty. The other parameters are as in Fig.14(a), except for Rsl=Rs=2/3 |
Conclusion
![]()
The results indicate that layers of similar thickness of totally-glued lubricant
molecules generally produce a smaller friction than lubricant molecules that are
head-glued. Totally-glued lubricants also stick better to the substrates, and
boundary layers thereof may accordingly be harder to squeeze out under high
load. On the other hand, whenever the applied load becomes strong enough to
squeeze the lubricant out to less than two molecular layers, then the head-glued
kind behaves much better in sustaining smooth sliding and low friction even at
very small residual coverage. We predict that when such extreme-load situations
are likely to occur in a practical lubricated sliding devices, head-glued
molecules could provide the best lubricant. Moreover, when the base lubricant
is totally-glued as a typical oil and, therefore, provides low friction
properties, then even a small concentration of head-glued additives may prevent
the substrates from wearing at places (asperities) where the surfaces come close
to each other within a thickness of less than two layers.
Similarly, friction shows a clear increasing trend as a function of molecular length L (this result is similar to the L dependency of the bulk viscosity). This would make monoatomic liquids the best lubricants, if it was not for their much reduced resistance against squeeze-out, which eventually makes polyatomic chains more effective lubricants at loads where boundary lubrication matters. Thus, the search for the best compromise between the necessity of a squeeze-out resistance, calling for large L, and of low-friction characteristics, calling for small L, is a rather intricate task.
For more details, see O.M. Braun, N. Manini, and E. Tosatti, Phys. Rev. B 78 (2008) 195402 "Role of lubricant molecular shape in microscopic friction" (pdf files may be found here)
Last updated on November 7, 2008 by O.Braun. Translated from LATEX by TTH