Tribology: An Introduction

Definition: The word tribology is derived from the Greek word tribos, meaning rubbing ("to rub"); thus, a direct translation of "tribology" is "the science of rubbing". However, now tribology incorporates also the studies of adhesion, contact formation, wear, fracture, lubrication, nanoindentation and, first of all, friction.

Historical remarks: The macroscopic laws of the classical (macroscopic) friction were found by da Vinci, Amontons, Euler and Coulomb.

Leonardo da Vinci (1452-1519) made experiments on an inclined plane. He found that friction is independent on the area of contact.

The law of Leonardo appears quite bizarre: Intuitively one would expect the friction force to be proportional to the area of contact. The paradox was resolved by Bowden and Tabor (~1950, see below), distinguishing between the real area of contact and the geometric (visible) area of contact. The real area of contact is only a small fraction of the visible area of contact.
Guillaume Amontons (1663-1705) have done experiments on a horizontal surface and measured the friction force with a spring. He observed that if double or triple the weight of the log, the friction is also doubled or tripled respectively. Thus, friction is proportional to the normal force (load) (and independent on the area of contact). Amontons called the proportional factor friction constant.
Leonard Euler (1707-1783) pointed that one has to distinguish between the static and kinetic friction: da Vinci tested the static friction, while Amontons dealt with the kinetic friction.
Charles Coulomb (1736-1806) measured the kinetic friction for different speeds and found that friction is independent on the velocity.

Why friction is important
Hydrodynamic and boundary lubrication
Experimental techniques
Results and laws for solid-on-solid friction
Important notes
Macroscopic theory
Stick-slip motion and smooth sliding
- A phenomenological theory
Low-dimensional models
Three-dimensional model (next Section)

Why friction is important

In one type of problems we have to maximize friction, for example,

(a) at ancient times (200,000 BC) – frictional heating in the lighting of fires by rubbing wood on wood;

(b) nowadays – pins (bolts etc., the static friction) or braking (kinetic friction between the car tires and the road).
More often the most important is to lower friction, for example,
(a) Egyptians (2,400 BC) used water to lubricate wooden sledges used to transport large stones to build the pyramids;

(b) nowadays – in machines, e.g., car engines. An example (from Persson's book): in USA friction takes away about 6% of the gross national product

Hydrodynamic and boundary lubrication

Hydrodynamic (fluid) lubrication (Reynolds 1886) – for a (macroscopically) thick liquid layer (e.g., 0.01 mm)
- use Navier-Stokes equations with appropriate boundary conditions (typically stick = locked);
- the friction is determined mainly by the viscosity of the liquid lubricant;
- an example (from Persson's book): Which lubricant is better – oil (with high viscosity) or water? A drop of water between clean hands does not make the hands slip easily over each other, while a drop of oil does. Why? The fluid is squeezed out from the contact area, but this process will take a long time if the viscosity is large.
Boundary lubrication – for a thin (few Angström) lubricant film, e.g., if the lubricant was squeezed out from the contact area
- the friction is typically much higher, e.g., by a factor of 10², as compared with the hydrodynamic lubrication;
- the friction mainly depends not on lubricant viscosity but on the chemical composition of the fluid; usually the better lubricant corresponds to a fluid that is adsorbed by the solid substrates.

At stop/start, (almost) always the regime of boundary lubrication occurs. In what follows we consider the boundary lubrication only.

Experimental techniques

(1) Standard technique (Bowden and Tabor 1950; Rabinowicz 1965; surface forces apparatus by Bhusham, Israelachvili, Landman, Granick; experiments with paper on paper by Heslot et al)

typically in air
the solids may be well defined as, e.g., for atomically flat mica plates
the separation between the surfaces may be controlled using optical interferometry (it can be measured to within ~1Å by studying multiple beam interference finger)
measured: spring force ("tribological" friction μ ≡ F_friction/F_load)
control parameters:
- v_spring (pulling velocity)
- k_spring (machine stiffness)
- F_load (loading mass)
- T (temperature)

(2) STM/AFM/FFM: scanning tunneling microscope (Gerd Binnig & Heinrich Rohrer 1981, Nobel Price 1986) for conducting surfaces, and atomic-force microscope (Binnig et al 1985) for dielectric surfaces – measure surface topography; friction-force microscope (Mate et al 1987) measures forces transverse to the surface

can be done in ultrahigh vacuum
typical tip radius is 10 nm to 100 nm
typical F_load ~ 10 nN to 150 nN
typical measured frictional forces F are less than or about 10^–11 N
typically operates at low velocities (v ~ 1 nm/s to 1 μm/s)

(3) Quartz-crystal microbalance (QCM) technique (Krim and Widom 1986): Gas atoms, such as Kr, Xe, or Ar, condense onto the surface of a quartz-crystal oscillator covered by a (111) oriented noble-metal substrate such as Au or Ag. The added mass of the adsorbate and the dissipation due to slip of the layer over the substrate shift and broaden the microbalance resonance peak. By measuring these changing, information about the form and magnitude of the frictional force can be obtained

can be done in ultrahigh vacuum
typically for one-two adsorbed layers only

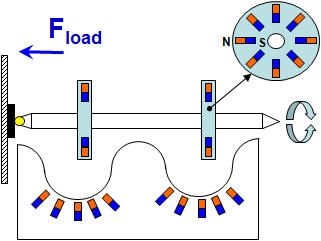
(4) Levitating tribometer (O.A. Marchenko & V.S. Kulik, Institute of Physics NASU; see movie)

up to submonolayer lubricant films
both surfaces and film structure may be controlled with STM/AFM before and after measurments!
low loads

(5) Molecular dynamics (MD)

atomic-scale; atomic trajectories
competition "size ↔ time"
too high velocities (typically v > 1 m/s)

Results and laws for solid-on-solid friction

μ ≡ F_friction/F_load ≈ constant, and μ is less than or about of 1 (Amontons 1699) → real (actual) contact area A_real~F_load (Philip Bowden & David Tabor 1950). Indeed, real surfaces are rough. Thus, A_real will grow until the external loading force will be balanced by the contact pressure integrated over A_real.
Let P_load^(real)= P_loadA/A_real be the real pressure at the contact. Then:
- at low P_load^(real)< P_yield (elastic regime) the number of contacts increases with load
- at high P_load^(real)> P_yield (plastic regime) the area of one contact increases (linearly) with load
μ_kinetic< or << μ_static, and μ_kinetic is approximately independent of the driving velocity v
Stick-slip motion ↔ smooth sliding
- stick-slip motion for soft systems and/or low velocities
- smooth sliding for stiff machines and/or high velocities
"Memory/age" effects: frictional forces depend on the previous dynamical history of the solid-solid contact, e.g., μ_static(t) ≈ a_s + b_s ln(t) and μ_kinetic(v) ≈ μ_static(a_φ/v) with the characteristic length a_φ~1 μm (due to plasticity of the system)
Full (large-scale) MD simulation showed that the lubricant structure may be
- liquid (low kinetic friction, f_static=0)
- amorphous (high frictions)
- solid (may be very low kinetic friction = superlubricity)

Important notes (what is known already)

Contacts / junctions / asperities:
- areas of real atomic contact between the two solids are small
- the contacts are randomly distributed in space over the area of apparent contact
- a typical contact size is 1 to 10 μm (may be measured optically)
An example (from Persson's book): Put a steel cube of 10 × 10 × 10 cm³ on a steel table. Taking P_load^(real) ~ P_yield≈ 10⁹ N/m², we obtain A_real~ 0.1 mm², so that ~10³ to 10⁵ junctions are expected at the interface. Note: STM/AFM/FFM techniques just study a single contact.
Forces are of atomic-scale value – close to the plasticity threshold. Estimation:
- a force per atom is f ~ 1 eV / 1 Å = 10^–19 J / 10^–10 m = 10^–9 N
- STM/AFM/FFM: area of one contact is A ~ 3 Å²; taking P_yield ≈ 0.2 GPa (gold) to P_yield ≈ 100 GPa (diamond), we obtain F ~ P_yieldA ~ 6·10^–12 N to 3·10^–9 N
- the hardness of the contacts is (much) larger than that of the material itself, because there are no dislocations in the (very small) stressed volume
- thus, (almost) always a deformation (either elastic or plastic) occurs at the contacts; this also explains Amontons law (Bowden and Tabor 1950): μ ~ F_yield ^(shear)/F_yield^(plastic) ~ 1 and is independent on the surface area.
(Almost) always there is a lubricant between the solids (called "third bodies" by tribologists): either a (specially chosen) lubricant film, or grease (oil), or dust, or wear debris produced by sliding, or water or/and a thin layer of hydrocarbon etc. adsorbed from air. Thus, the frictional force is almost entirely determined by the force required to shear the lubricant film itself.
(Almost) always the lubricant and the solids are "incommensurate":
- the lattice constants do not coincide in a general case
- the angles: the direction of sliding is generally at some angle to the surface lattice, and
  
  the two surface lattices are not generally in registry
- but the situation is not so trivial – often the lubricant atoms are "glued" (grafted) to the substrates (to avoid the flow of the lubricant out from the contact region), thus in fact we typically have an interface between the "glued" lubricant layer and other lubricant layers, thus the interface may be commensurate.
A thin film (less than 10 molecular diameters) is (almost) always layered, because the plates induce crystalline order in the film (solidify / freeze the lubricant; Thompson et al 1995). Moreover, when the lubricant thickness is less than three layers, most films behave like solid (glass-like in most cases, although may be ordered for relatively simple lubricant molecules).

See also an interesting tutorial with movies at Nano-World - a Swiss Virtual Campus Project

Macroscopic theory (Bowder & Tabor 1950)

Assume that the yield stress τ_s at the contact is linearly coupled with the local pressure p,

τ_s(p) = τ₀ + αp.

Then, integrating over the area of real contact, we obtain

F_friction= τ₀A_real + αF_load

and

μ = α + τ₀/,

where = F_load/A_real. Amontons' law operates if either >> τ₀, or if is constant, the latter holds for the ideally plastic surfaces (when = P_yield) as well as for elastic surfaces (Volmer and Natterman 1997: real surfaces are self-affine fractals, thus as F_load increase, the old contacts are expanding and new contacts are created). Finally, the real area of contact must become equal to the apparent area, and Amontons' law will not operate. It is so for rubber but not for steel – a machine would be destroyed earlier.

Stick-slip motion and smooth sliding

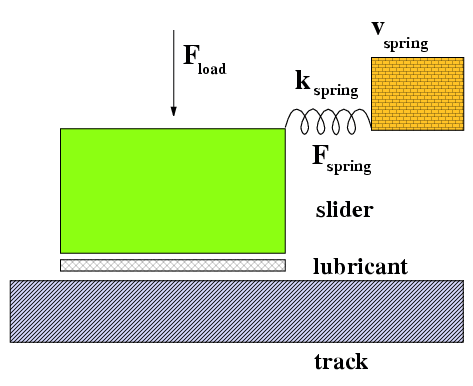
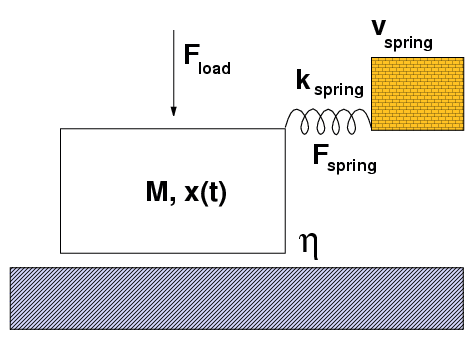
In a typical experiment as well as in real machines, a spring is attached to the slider (even if there is no spring, the elasticity of the block plays the same role). The free end of the spring moves with a velocity v_spring, and the force in the spring is registered.

Let initially the system is in rest and the spring has its natural length. Then when the base moves, the spring stretches, f increases until the threshold value f_s (the static frictional force), and the block starts to move. Then due to inertia, the slider accelerates to catch the base. If v_spring is small, f decreases until the "backward" threshold force f_b, and the slider stops. Then the process repeats, so the stick-slip motion occurs. Otherwise, when v_spring is large, the smooth sliding takes place.

low velocity &/or soft system high velocity &/or stiff system

Experiment: the behavior depends on the values v_spring and k_spring. The smooth sliding is observed if the spring is stiff enough, and/or if the velocity is high enough. Otherwise, the stick-slip motion is observed. During stick, the elastic energy is pumped into the system by the driving device; during slip, this elastic energy is released into kinetic energy, and eventually dissipated as heat.

Note: if one assumes that the frictional force depends on the instantaneous velocity only, f_fric= f(v), then the boundary separating two regimes corresponds to the vertical line in the (v_spring, k_spring) plane (i.e., the critical velocity is independent of k_spring), that is wrong. Thus, "memory" effects must be included.

(a nice applet written by F.-J. Elmer clearly demonstrates stick-slip and smooth motion)

Phenomenological theory

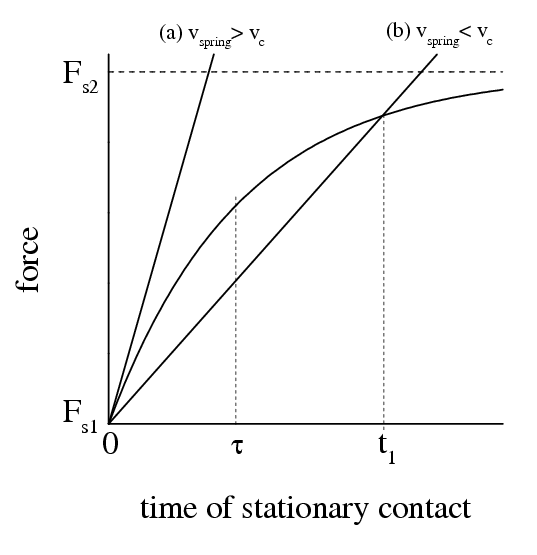
The phenomenological model of the transition "stick-slip motion « smooth sliding" has been developed by Heslot et al 1994, Baumberger et al 1994, and Persson 1997. The model is based on the assumption that the static frictional force depends on the time of stationary contact. For example, if the sliding-to-locked transition has occur at t=0, then the static frictional force will evolve as

f_s(t) = f_s1 + (f_s2–f_s1)(1–e^–t/τ),

(*)

so that just after the locking the force is f_s(0) = f_s1, but later, at t → ∞, it approaches the value f_s(∞) = f_s2> f_s1.

Qualitatively (Persson): In case (a) the spring force increases faster with t than the initial linear increase of the static frictional force; hence the motion of the slider will not stop and no stick-slip motion will occur; In case (b) the spring force will be smaller than the static frictional force until t reaches the value t₁ at which time slip starts; hence stick-slip motion will occur. Thus, the critical velocity is determined by the initial slope of the dependence f_s(t),

v_c ~ k_spring^–1 df_s(t)/dt|_t=0

The phenomenological model includes two differential equations: The motion of the top block is described by the equation

(t) + M η

(t) + f_fric[x(t)] = f_drive[x(t)] = k_spring [v_springt – x(t)],

where x(t) is the coordinate of the sliding block, M is its mass, and η is a phenomenological coefficient describing the viscous damping when the block slides over the bottom block. The second equation has to describe the frictional force f_fric[x(t)]. The idea is to introduce some artificial variable called the "contact-age function" φ(t) which depends on the prehistory of the system, and is defined by the following differential equation,

(t) = 1 –

(t) φ(t)/a_φ

where a_φ is some characteristic distance of microscopic-scale order, e.g., the substrate lattice constant a. Then one assumes that f_fric[x(t)] in equation for the top block is determined by Eq.(*) where, however, instead of time one has to substitute the contact-age function φ, instead of f_s1, the backward force f_b, and instead of f_s2, the static frictional force f_s, so that

f_fric[x(t)] = f_b + (f_s– f_b)( 1 – exp{–φ[x(t)]/τ} ).

(**)

Thus for the stationary contact we have φ(t) = t and we recover the dependence Eq.(*), while for the steady sliding regime φ = a_φ/v_spring= τ_v(v_spring) does not depend on time (τ_v is the average time a junction survives before being broken by the sliding motion), and the force f_fric(v) = f_b + (f_s– f_b)[1 – exp(–a_φ/v_springτ)] is the constant dependent on v_spring, it is large at low velocities, f_fric= f_s for v_spring→0, and small at high velocities, f_fric= f_b for v_spring→ ∞. This set of equations leads to smooth sliding for large v_spring and to stick-slip motion at low velocities. Using the parameters M, k_spring and v_spring corresponded to an experimental setup, taking some reasonable values for the forces f_b and f_s, and playing with the phenomenological parameters τ, η and a_φ, one can achieve excellent agreement with experimental results. However, while the dependence Eq.(*) can be explained with physical models, the phenomenological dependence Eq.(**) has no good physical background, it does not follow from simulation.

Low-dimensional models

Zero-dimensional model – one atom in the periodic substrate potential: the rigid bottom substrate (external sinusoidal potential) + one atom + the dc force is applied directly to the atom + Langevin motion equation + underdamped external friction

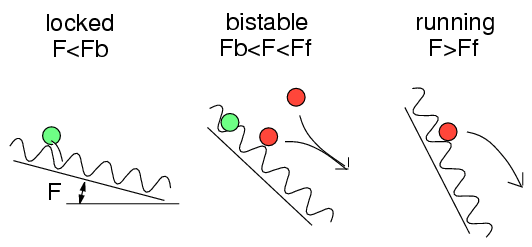
One-dimensional models:

Tomlinson model	Frenkel-Kontorova model

(nice applets for the Tomlinson model and the dc driven FK model were written by F.-J. Elmer)

More complicated models:

Tomlinson + FK (Elmer et al)
Two FK chains (J.Röder et al)
The FK chain between two external sinusoidal potentials (Rozman et al)
Random substrate/springs (overdamped FK model, Cule and Hwa 1996) → directed percolation

Two-dimensional models

2D(||) models: 2D layer of atoms on the 2D periodic substrate. Variants:
- Springs and balls models: dislocation lines, instabilities
- Scalar anisotropic 2D model: system of coupled 1D FK chains
- Vector anisotropic 2D model: zigzag kinks
- Vector isotropic 2D model (Persson 1993, 1994; our simulation)
2D(_┴) model (Hammerberg et al): creation of dislocations at the interface; cracks

Next: 3D model

Back to main page or tribology page

Last updated on October 15, 2008 by Oleg Braun. Translated from L^AT_EX by T_TH