Equation of motion:
|
where V(x) = V0 exp(–βx). Limits:
β→ 0 harmonic interaction
β→ ∞ hard-core interaction
Continuum approximation (Rosenau 1986):
|
The steady-state
solution for every value of f satisfies the "automodel" condition:
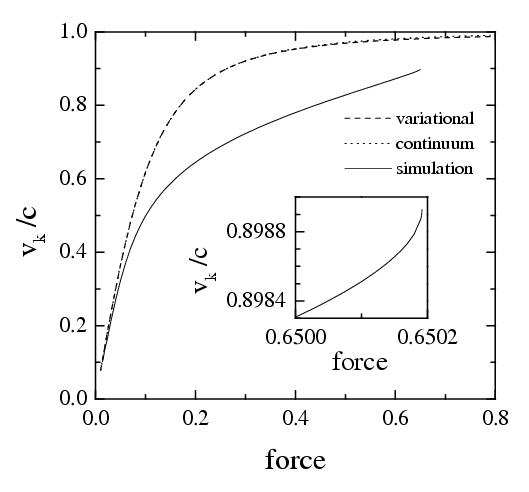 |
Figure: The kink velocity vk as a function of the driving force f for g=1, η=0.1, and N=128. The dashed curve corresponds to the SG dependence, and the dotted curve, to the kink velocity in the continuum limit approximation. |
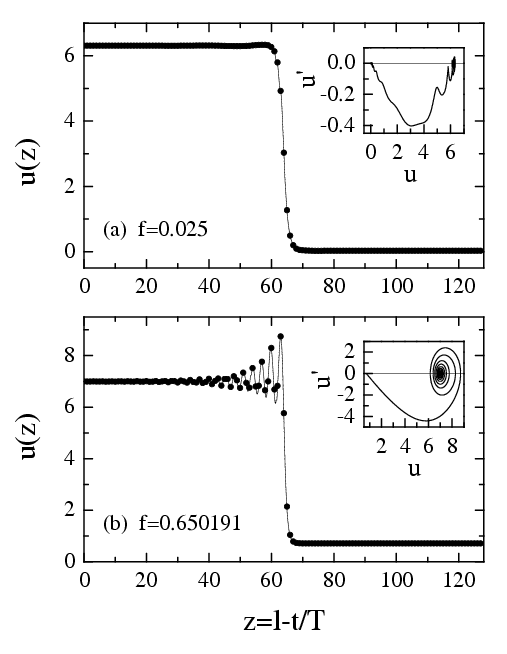 |
Figure: Kink's shape in the discrete
chain as a function of
(a) a small force f=0.025 and
(b) the critical force f=0.650191 (g=1, η=0.1, N=128, M=64).
Black circles show instantaneous atomic positions and the solid curve corresponds to the "automodel" curve.
Inset: the corresponding separatrices. |
A dynamical shape mode, or discrete breather is excited close to the critical force.
 |
 |
||
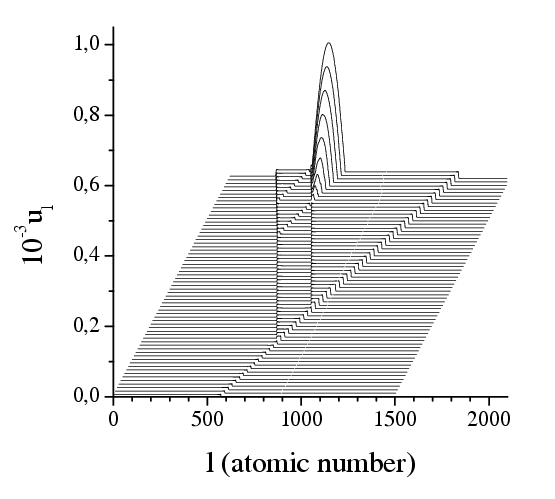
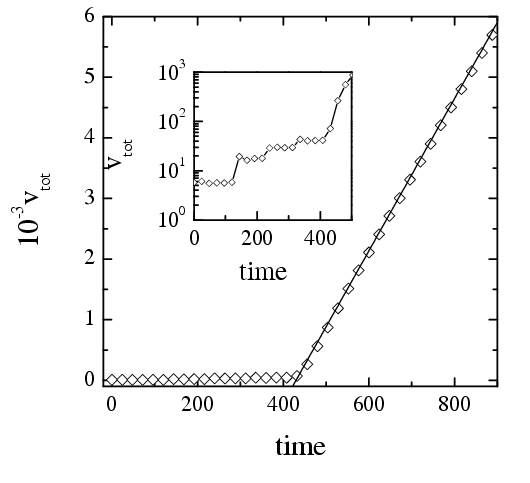
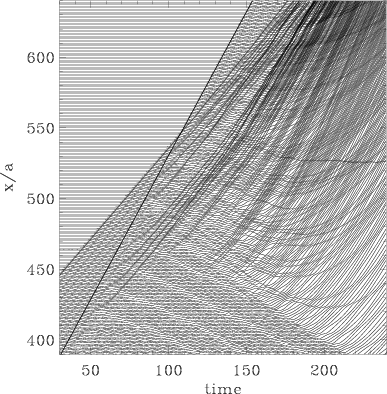
| Figure: Evolution of the system at f=0.651 starting from the initial state corresponded to the steady state for f=0.65, when vk≈ vcrit. The system parameters are g=1, h=0.1, and N=1500 (enlarged view). | Figure: The dependence vtot(t)
for the system evolution at f=0.651. The solid line describes the
fit |
||
For details see the paper by O.M. Braun, Bambi Hu, and A. Zeltser, Phys. Rev. E 62 (2000) 4235 "Driven kink in the Frenkel-Kontorova model" (pdf files may be found here)
If the structure is commensurate (no kinks in the GS), then the first event is the (thermally activated and force stimulated) creation of a kink-antikink pair; then the scenario is the same.
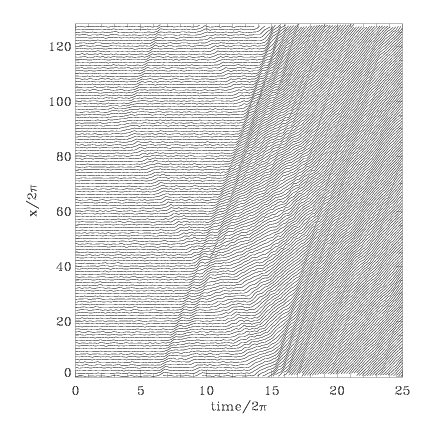
Figure: Atomic trajectories for the commensurate FK model with exponential interaction at f=0.53 and T=0.7 (geff=1, η=0.1, N=128)
See O.M. Braun, A.R. Bishop, and J. Röder, Phys. Rev. Lett. 79 (1997) 3692 "Hysteresis in the underdamped driven Frenkel-Kontorova model" (pdf files may be found here)
If the GS is not trivial (θ < 1) then the transition is multi-step:
locked state → running kinks → TJ state (creation of kk pairs) → running (sliding) state
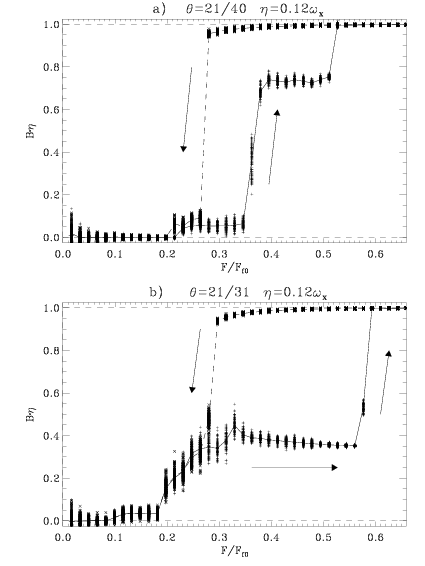 |
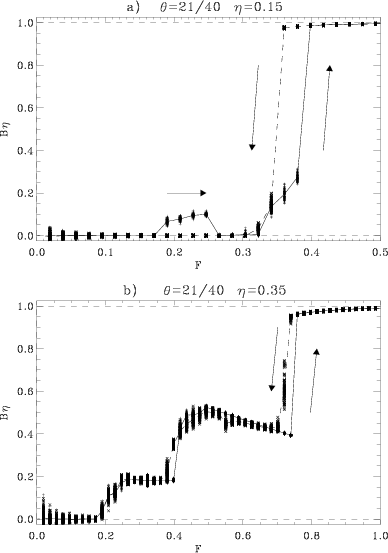
Figure: The mobility B = ‹v›/f versus the force f for the underdamped (η=0.12) FK model with exponential interaction (geff=0.58)
(a) for θ=21/40 (trivial kinks on the background of trivial θ0=1/2 structure), and
(b) for θ=21/31 (superkinks on the background of the complex θ0=2/3 structure)
|
The locked-to-sliding transition in the FK model has been studied in a series of papers (pdf files may be found here):
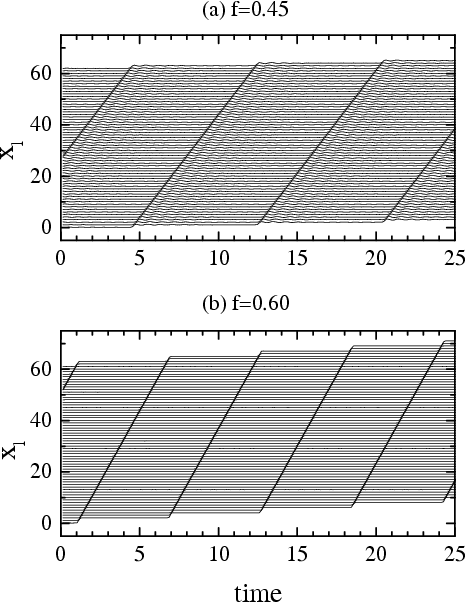 |
(a) the single supersonic kink (f = 0.45, vk/c =1.28)
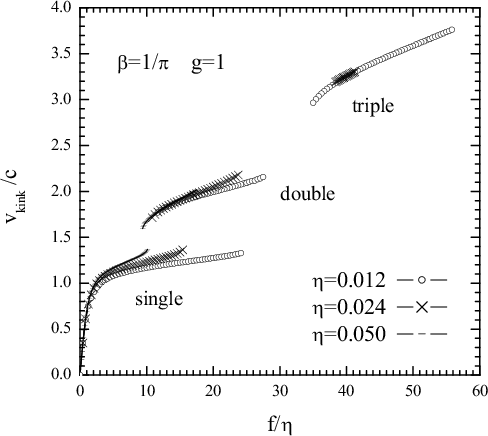
Atomic trajectories of the FK model with exponential interaction (β=1/π, g=1, η=0.05)
(b) the double kink (f = 0.60, vk/c =1.75)
|
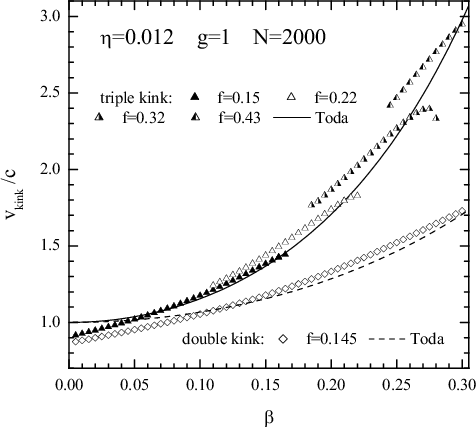
| The double kink | The triple kink |
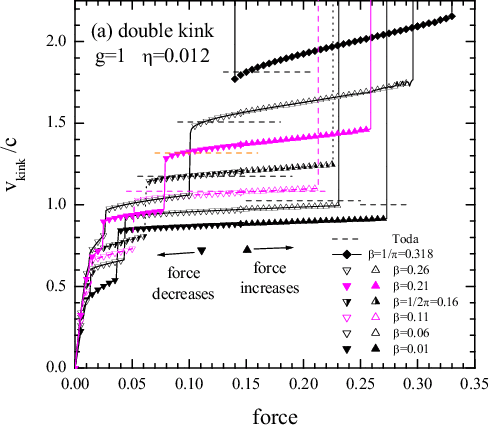 |
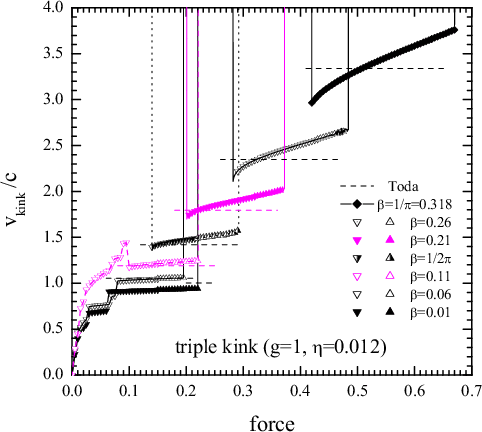 |
| enlarged view | enlarged view |
Multiple kinks exist due to discreteness of the FK chain:
even for the classical model (β = f = η = 0), when the single kink is pinned due to the PN barrier,
the double kink propagates with a fixed velocity vk/c = (2/3)1/2 (Champneys & Kivshar 2000)
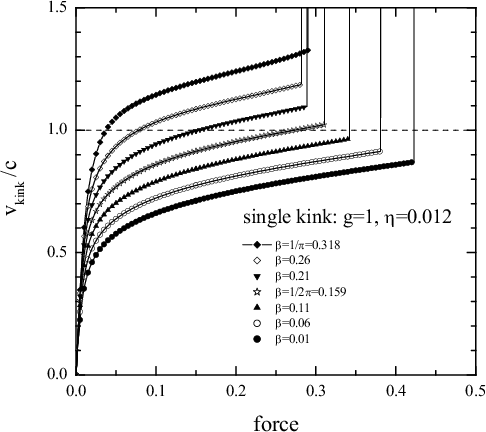 |
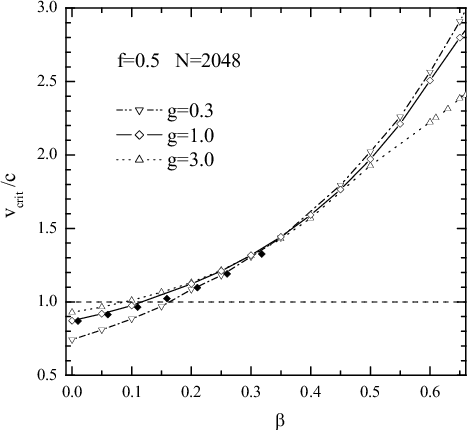 |
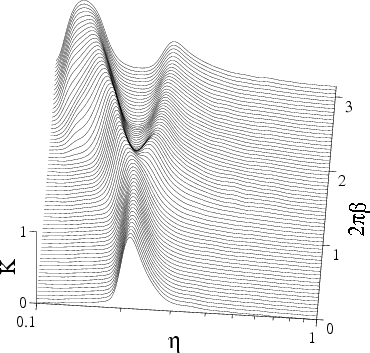
The velocity of the single kink versus the force (β=1/π, g=1, η=0.05) |
The critical kink velocity vc(β) at the fixed force f = 0.5 |
Anharmonic interaction: (multiple) kinks ≈ Toda solitons:
 |
|
|||
 |
|
 |
if the
stability intervals
overlap:
single
kink + double kink →
triple kink
(β=0.01,
f=0.15,
g=1,
η=0.012)
|
 |
if the
stability intervals
do not overlap:
single
kink + double kink →
running state
(β=1/π,
f=0.25,
g=1,
η=0.012)
|
More results on multiple and supersonic kinks may be found in the papers (pdf files may be found here)
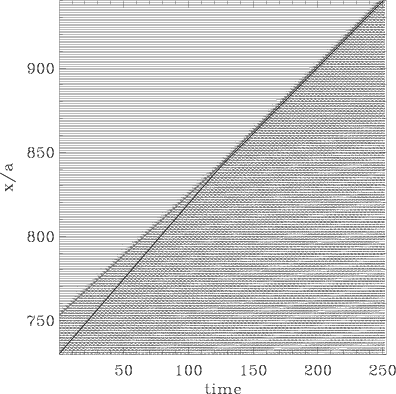
| Atomic trajectories for β = 1/π, f = 0.33 | Zoom of the rectangle on the left figure |
 |
 |
Schematically:

|
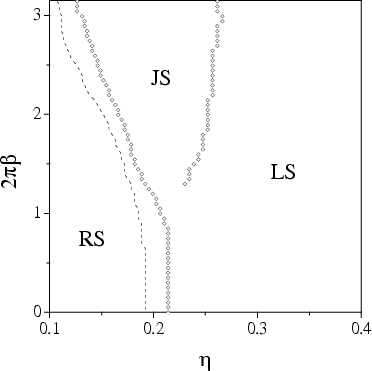
Phase diagram (N=256, g=0.1, f=0.5, T=0.1) |
Section of the left figure |
 |
 |
Traffic jams do appear in the underdamped FK model with anharmonic interaction just before the transition to the running state, if the following conditions are satisfied:
(1) It must be an external (substrate) potential, either periodic or random;
(2) The motion must be underdamped, the particles should have two different states, the locked state and the running state;
(3) It must be some randomness in the system (either an intrinsic chaos, or T > 0);
(4) The particles must interact, and this interaction has to be anharmonic (already the hard-core potential is sufficient to produce the traffic-jam behavior).
See the paper by O.M. Braun, B. Hu, A. Filippov, and A. Zeltser, Phys. Rev. E 58 (1998) 1311 "Traffic jams and hysteresis in driven one-dimensional systems" (pdf files may be found here) and also the web page "Driven Lattice-Gas Model"
In the soft FK model, the particles have a complex structure treated in a mean-field fashion: particle collisions are inelastic and also each particle is considered as having its own thermostat. The model has a truly equilibrium ground state. When an external dc force is applied to the atoms, the model exhibits a hysteresis even at high temperatures due to the clustering of atoms with the same velocity. Another effect of clustering is phase separation in the steady state when the system splits into regions of immobile atoms ("traffic jams") and regions of running atoms.
Idea: Consider a system consisting of complex particles, which have their own structure with internal degrees of freedom. The internal modes may be excited due to inter-particle collisions, that take away the kinetic energy of the translational motion, so that the collisions are inelastic. This is a typical situation in soft-matter physics, for example, in physics of granular gases. The kinetic energy of atomic translational motion that is lost in a collision is stored as the energy of excitation of internal degrees of freedom and may be released later as the kinetic energy. In a simple case, when the number of internal degrees of freedom is “large” and their coupling is nonlinear, the energy lost in collisions is transformed into the “heating” of particles. We propose a new type of stochastic models, a model with “multiple” thermostats, where, in addition to the standard “substrate” thermostat, each particle is considered as having its own “thermostat”. A natural description of such a model is one with a specific type of Langevin equations (or the corresponding Fokker-Planck equation).
Motion equations: The equation of motion for the lth particle has the form
|
where the dot (prime) indicates the time (spatial) derivative. The substrate thermostat is modeled by the Gaussian stochastic force δFl(t) which has zero average and the standard correlation function
|
|
(a1) |
|
The mutual damping hl was chosen to depend on the distance between the NN atoms in the same way as the potential, hl = h*exp[-g (xl- xl-1- aA)], where h* is a parameter which describes the inelasticity: the interaction is elastic in the case of h*=0, while in the limit h*→ ∞ the collisions are completely damped.
This set of Langevin equations is equivalent to the Fokker-Planck-Kramers equation for the distribution function W,
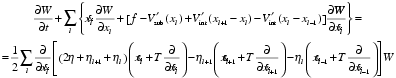
It is easy to check that in the undriven case, f = 0, the Maxwell-Boltzmann distribution is a solution of the FPK equation. Thus, the model has the truly thermodynamically equilibrium state.
Simulation results:
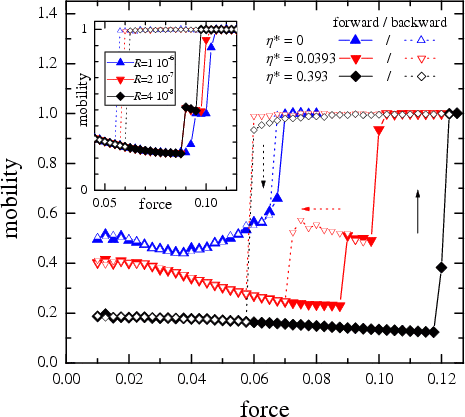
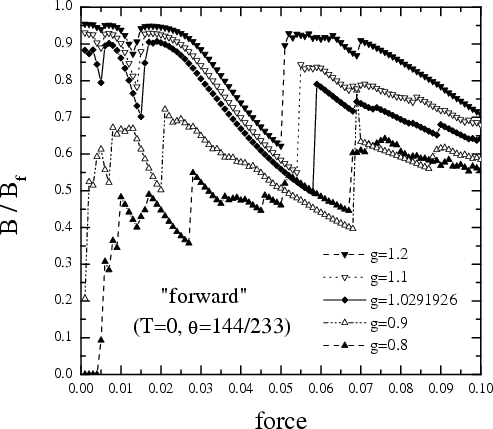
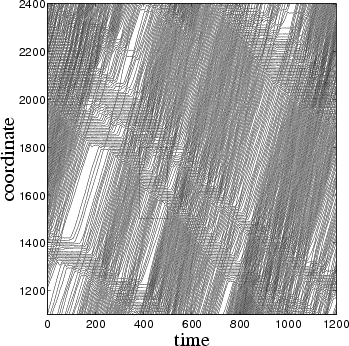
Figure: Dependence of the normalized mobility B on the force f for three values of the intrinsic damping: h*=0 (blue up triangles, the "elastic" model), h*=e-aA » 0.0393 (red down triangles), and h*=10 e-aA » 0.393 (black diamonds) for an increasing force (solid curves and symbols) and a decreasing force (dotted curves and open symbols). Other parameters are the following: N/M = 144/233 = golden mean, g = 1/p, g = 1, h = 0.01, and T = 1. Inset: B(f) for h* » 0.0393 for three values of the rate of force changing: R » 10-6 (blue up triangles), R » 2·10-7 (red down triangles), and R » 4·10-8 (black diamonds).
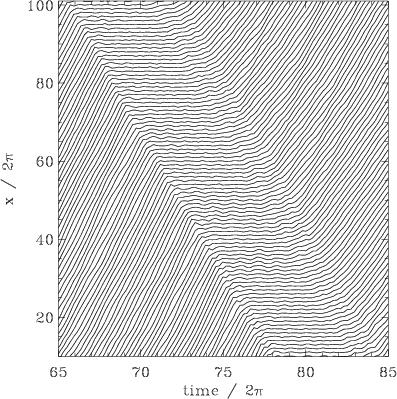
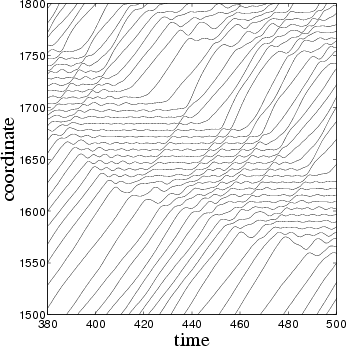
Figure: Atomic coordinates as functions of time in the "traffic-jam" regime for f = 0.095, h*» 0.0393, g = 1/p, g = 1, h = 0.01, and T = 1.
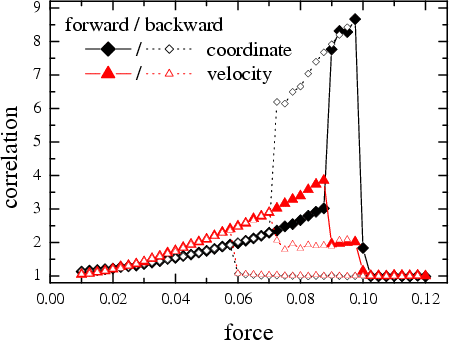
Figure: Dependence of the normalized correlation of coordinates Kx/Kx0 (black diamonds) and velocities Kv/Kv0 (red triangles) on the driving force f for h*» 0.0393, g = 1/p, g = 1, h = 0.01, and T = 1 for an increasing force (solid curves and symbols) and a decreasing force (dotted curves and open symbols). Note that for a spatially homogeneous state we should have Kx » Kx0 = T/g and Kv » Kv0 = 2T.
Conclusion: The dynamics of the soft model with inelastic interaction drastically differs from the classical (elastic) one. First, the system exhibits hysteresis even at huge temperatures. The reason why the 1D model exhibits hysteresis is that the soft model is effectively infinite-dimensional. The particles have an infinite number of internal degrees of freedom treated in a mean-field fashion. Second, the soft model allows the coexistence of two phases (the TJ regime) for a much wider range of model parameters. Both effects are due to the clustering of atoms in the soft model.
|
 |
 |
|
|
| small damping |
 |
 |
|
| larger damping | |
| enlarged view |
(exponential repulsion, β = 0.37, geff = 0.15)
Dynamical phase diagram:
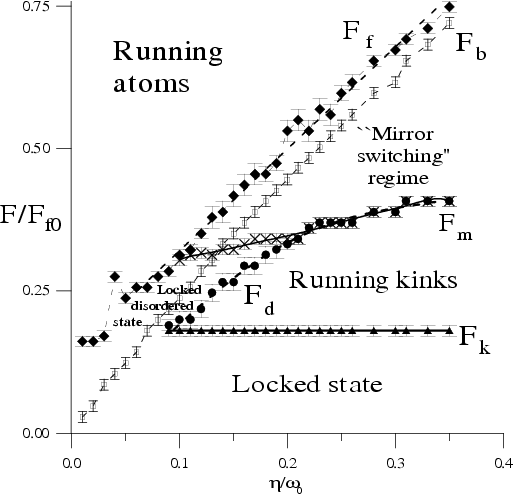 |
enlarged view |
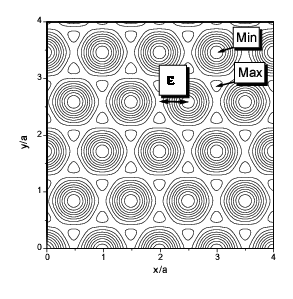
We also studied the nonlinear dc response of a two-dimensional underdamped system of interacting atoms subject to an isotropic periodic external potential with triangular symmetry. When driving force increases, the system transfers from a disorder locked state to an ordered sliding state corresponded to a moving crystal. By varying the values of the effective elastic constant, damping and temperature, we found different scenarios and intermediate phases during the ordering transition. For a soft atomic layer, the system passes through a plastic-channel regime that appears as a steady-state regime at higher values of the damping coefficient. For high values of the effective elastic constant, when the atomic layer is stiff, the intermediate plastic phase corresponds to a traffic-jam regime with immobile islands in the sea of running atoms. At a high driving of the stiff layer, a soliton-like elastic flow of atoms has been observed.
Movies:
A. Locked-to-sliding transition for g=0.1, η=0.1, T=0.1, F changes from F=0.355 to F=0.4: avi 21 Mb
B. Steady states for:
g=0.1, η=0.3, T=0.001, F=0.645: animated gif 5.5 Mb (channel plastic flow)
g=0.1, η=0.3, T=0.1, F=0.57: animated gif 3.9 Mb (traffic jams)
g=0.3, η=0.3, T=0.001, F=0.6: animated gif 3.1 Mb (traffic jams)
g=0.3, η=0.3, T=0.001, F=0.615: animated gif 3.8 Mb (channel plastic flow)
g=1, η=0.1, T=0.001, F=0.165: animated gif 3.4 Mb
g=1, η=0.1, T=0.001, F=0.35: animated gif 3.1 Mb (elastic flow)
g=1, η=0.3, T=0.001, F=0.4: animated gif 3.4 Mb
g=1, η=0.3, T=0.001, F=0.65: animated gif 2.6 Mb (solitonic, or DW motion)
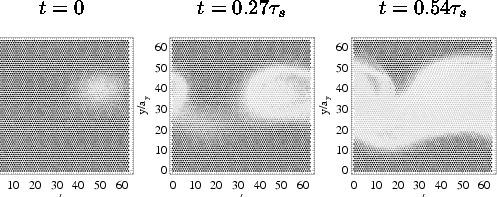
A. Stiff layer: geff ~ 1 or > 1 (example for LJ interaction with geff = 0.9, η = 0.141, T = 0.05, and f = 0.9933)
B. Weak layer: geff << 1 (example for exponential interaction with geff = 0.1, η = 0.1, T = 0.01, and f = 0.94)
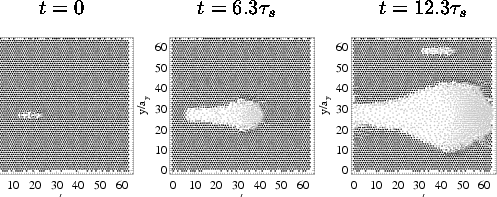
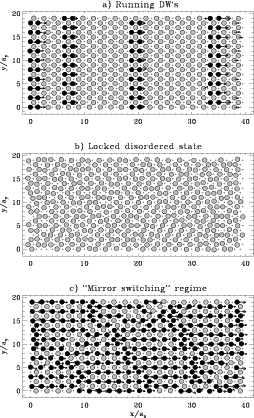
Figures: The positions of the particles are indicated by circles. The x component of the particle velocity is shown in a grey scale by the color of the circle: black corresponding to zero velocity and the lightest grey to velocities over a certain velocity cutoff.
For details, see also (pdf files may be found here)
O.M. Braun, M.V. Paliy, J. Röder, and A.R. Bishop, Phys. Rev. E 63 (2001) 036129 "Locked-to-running transition in the two-dimensional underdamped driven Frenkel-Kontorova model"
J. Tekic, O.M. Braun, and Bambi Hu, Phys. Rev. E 71 (2005) 026104 "Dynamic phases in the two-dimensional underdamped driven Frenkel-Kontorova model"
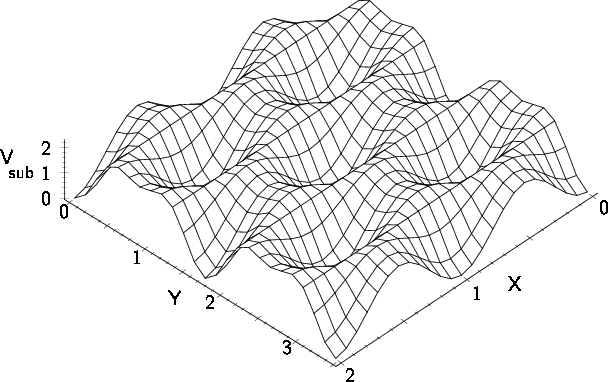
A simplified model: Vsub(x,y) = 1 – cos x + ½ ω2y2
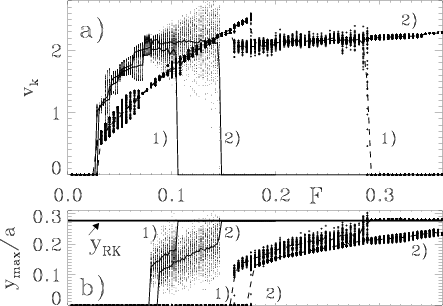
Figure: small dots & solid curves: η = 0.1; bold dots and dashed curves: η = 0.2;
labels: (1) θ = 64/56; (2) θ = 64/60
 |
 |
| enlarged view |
The fuse-safety device was introduced and studied in the paper by Oleg Braun, Maxim Paliy, and Bambi Hu, Phys. Rev. Lett. 83 (1999) 5206 "Fuse safety device on an atomic scale"
For the 2D FK model,
Ø θ < 1: a TJ state ?
Ø role of defects in the 2D model ?
Ø quasi-periodic / random substrate potential ?
a.c. driven underdamped models (1D & 2D) ?
ratchet scenarios?
Last updated on October 5, 2008 by Oleg Braun. Translated from LATEX by TTH