Mobility. Mass or charge transport in
one-dimensional anharmonic lattices is described by the flux
In the FK model, the mobility has minima at rational (commensurate) GS configurations
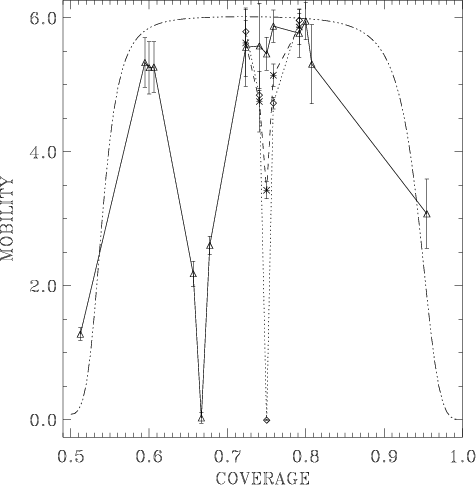
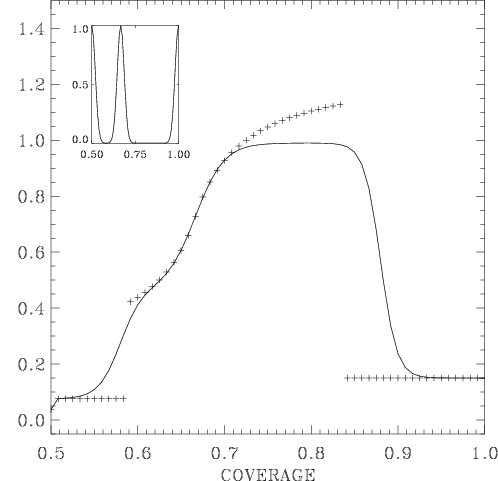
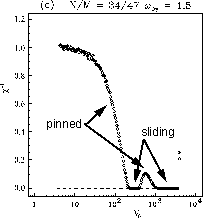
Figure: simulation results for the mobility B versus the coverage for the 1D model with V0=100 at different temperatures: T=0.005 (diamonds and dotted line), T=0.05 (asterisks and dashed line), T=0.1 (triangles and solid line). The dash-triple-dotted line is for the perturbative approach at T = 0.1,
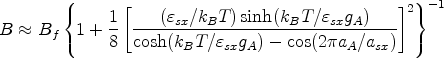
Chemical diffusion. Definition:
![]()
where <<...>> stands for average over mesoscopic distances.
Method I: Use the Einstein relation Dc = kBTB / χ, where χ is the (dimensionless) static susceptibility,

μ is the chemical potential, n is the atomic concentration, and Π is the pressure
Then we may use the ideal kink-gas ideology, where χ is given by
![]() ,
and
,
and![]()
![]()
Method II: Kink diffusion ≈ chemical diffusion. Idea:
| Dc = | flux
of atoms
|
≈ | flux
of kinks
|
= Dkink + |
|
|
|
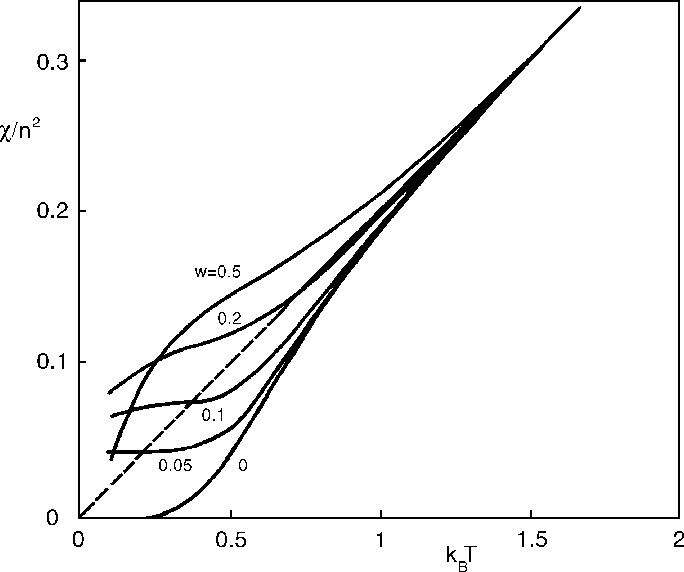
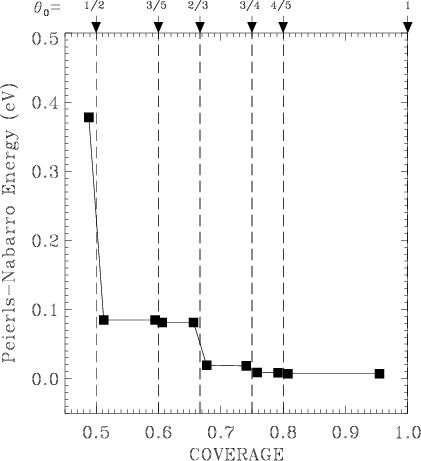
Simulation results for exponential interaction (see below):
| PN barrier vs concentration | Dc versus concentration |
 |
 |
More details may be found in the following papers (pdf files may be found here):
O.M. Braun, Thierry Dauxois, M.V. Paliy, and M. Peyrard, Phys. Rev. E 55 (1997) 3598 "Nonlinear mobility of the generalized Frenkel-Kontorova model"
O.M. Braun, Thierry Dauxois, M.V. Paliy, and M. Peyrard, Phys. Rev. B 54 (1996) 321 "Mobility and diffusivity in a generalized Frenkel-Kontorova model"
O.M. Braun and Yu.S. Kivshar, Phys. Rev. B 50 (1994) 13388 "Concentration dependence of conductivity and diffusivity in one-dimensional anharmonic lattices"
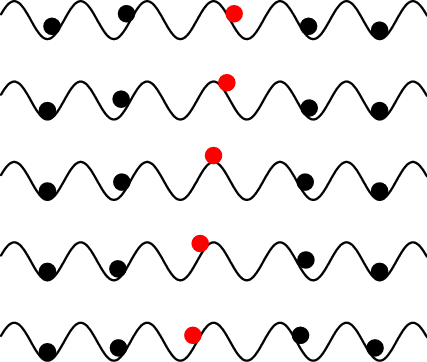
A. kink ≠ antikink
d2ul/dt2 + sin ul + V′(a+ul–ul–1) – V′(a+ul+1–ul) = 0
continuum approximation: xl(t) = la + ul(t), l → x=la, ul(t) → u(x,t)
anharmonic interaction: V′(a+u) ≈ V′(a) + V′′(a) u + ½V′′′(a) u2
utt + sin u – uxx(1 – αux) = 0, d2 = a2V′′(a), α = – (a/d)V′′′(a)/V′′(a)
u(x) = uSG(x) + Δu(x), Δu(x) ≈ (4α/3) tanh–1sinh(x)/cosh(x)
m ≈ (8/ad)[1 ± (π/6)α], EPN = EPN0 ± δEPN
 |
owing to anharmoncity of |
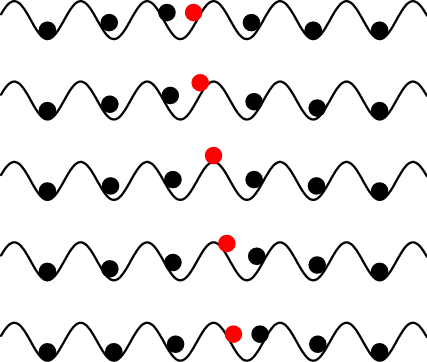 |
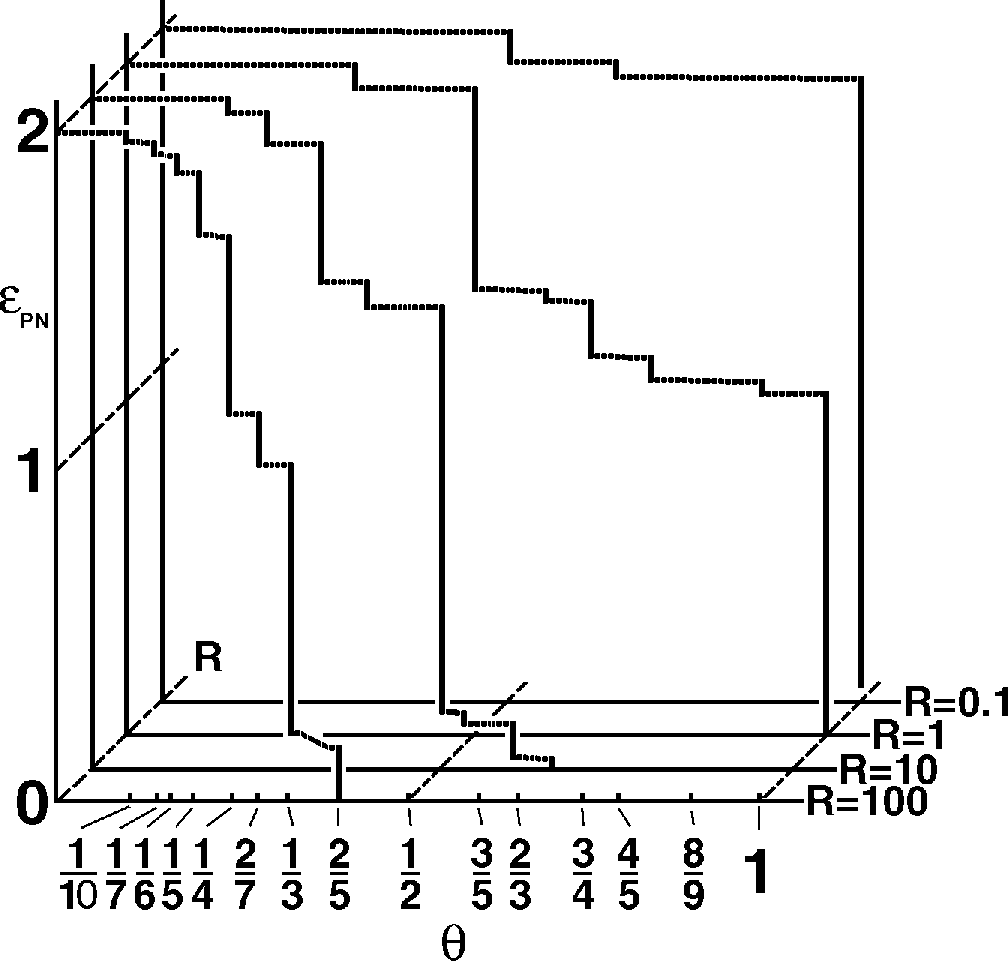
B. PN barriers – Devil's staircase: for any rational concentration θ0 = p/q, jump in the PN barrier:
EPN(θ0–0) – EPN(θ0+0) = δEPN > 0
See also the papers (pdf files may be found here):
Requirements on Hint{u1(x), u2(x)}:
(a) for |u1(x) – u2(x)| << as it must be Hint{u1,u2} ~ ∫dx [u1(x) – u2(x)]2
(b) Hint = inv at u2 → u2 + as
|
old configuration new configuration |
||
 |
→ |
 |
(c) Hint ≠ 0 if u1(x) ≡ u2(x) ≠ const
Hint{u1,u2} ~ ∫dx dx′ u1′(x) Vint(x–x′) u2′(x′), because ρ(x) = –as–1u′(x) is the density of "extra" atoms
Local approximation: Vint(x) → δ(x)
|
where
|
repulsion: α, γ > 0; attraction: α, γ > 0
anzats: un(x, t) = uSG(x; Xn(t)) = 4 tan–1exp{–[x–Xn(t)]/d}
Effective Hamiltonian:
|
where ε = md2 is the X-kink rest energy
m = 4/πd is the X-kink rest mass
εPN is the amplitude of PN barrier for X-kinks
Interaction between the kinks: V(X) = –ε[αW1(X/d) + γW2(X/d)], where
W1(Y) = (1 + Y/sinhY) tanh2Y and W2(Y) = (1 – Y/sinhY)
small displacement (|X| << as): V(X) ≈ ½GX 2, where G = –m(α + (⅓)γ)
large shift (X → ∞): V(∞) = –ε(α + γ) = Edissociation
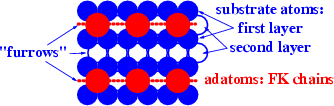
(a) If G < 0 (repulsion between the adatoms, α,γ > 0) and Ediss < 0, then repulsion between X-kinks: c(2x2) structure of X-kinks εA ≈ εPN(Y)< εPN so that D > D0 Cs or K on W or Mo(112) |
|
(b) If –3α < γ < –α < 0 then G < 0 and Ediss > 0: oblique Y-chains of X-kinks D > D0 if x0≈as(n+½) D < D0 if x0≈asn (n is integer) Li or Na on W or Mo(112) at 0.5 < θ << 1 |
|
(c) If G > 0 (α + ⅓γ < 0) then X-kinks attract each other: Y-chains of X-kinks εA ≈ εPN + (EY + EY) or εA ≈ εPN + Ediss Li on W or Mo(112) at θ ~1 |
|
See also the following papers (pdf files may be found here):
O.M. Braun and Yu.S. Kivshar, J. Phys.: Condensed Matter 2 (1990) 5961 "Kinks in a system of adatomic chains"
O.M. Braun, Yu.S. Kivshar, and A.M. Kosevich, J. Phys. C 21 (1988) 3881 "Interaction between kinks in coupled chains of adatoms"
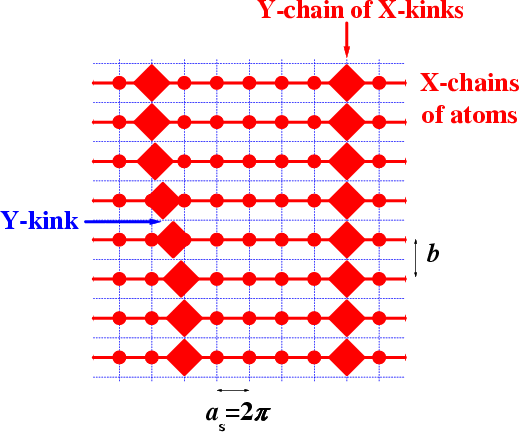 |
Parameters of Y-kinks: width: DY ≈ b(2G/εPN)1/2 Y-kink energy: EY ≈ π2G if DY << b ≈ (8/3)[–2πd(3α+γ)]1/2exp(–πd/4) if DY >> b PN barriers: EPN(Y) ≈ εPN – π2G if DY << b ≈ (16/3)π4G exp[–π2(2G/εPN)1/2] if DY >> b |
|
|
 |
|
|
|
|
|
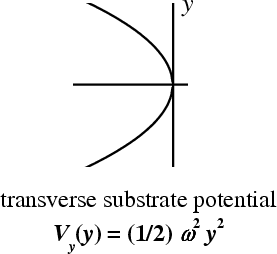
Example: for Coulomb repulsion as2ωy2 + 4Vint′(as) = 0, Vbif ≈ 0.25ωy2aA3
Existing of a transversal degree of freedom modifies
the ground state
topological excitations ("nonmassive" kinks, ε PN(θ))
Aubry transitions
and leads to predictions
Dc(θ) (down jumps at θ = θbif)
reconstructive scenario of crystal growth
complicated diffusion mechanism
displacements from
nearest
minima of Vsub(x)
|
average elastic constant
|
reverse Aubry transition f = 10–4 along x xl0 = displacements at f = 0 xl = displacements at f = 10–4 Δxshift = N–1 ∑(xl–xl0) c = Δxshift / f |
|||||
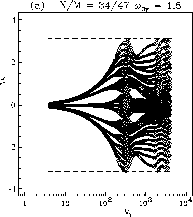 |
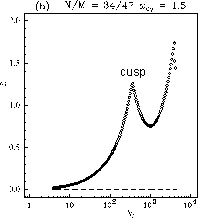 |
 |
Competition: Aubry VAubry= f(θ) ↔ Vbif ~ ωy
(a) ωy < ω*, gbif < gAubry , no Aubry transition
(b) ω* < ωy < ω**, gmin< gAubry< gbif , normal/reverse/normal Aubry transitions
(c) ωy > ω**, gAubry< gmin= min g(V), normal Aubry transition
(m.e. cnf)
|
 |
trivial GS V < Vbif (k)
zig-zag GS V > Vbif |
 |
| "nonmassive" (phase) kink |
 |
min-en. cnf |
| saddle cnf |
The case of Vbif (k)< V < Vbif : the bifurcation begins at the kink's core
utt + sin u – d2uxx(1 – αdux) = 0
trivial GS: kink width d0= (2π)(g + 4g1)1/2, α0= –(2π/d0)3[V ′′′(r0) + 8V ′′′(r1)] > 0
zigzag GS: kink width d = (2π)(4g1– ¼ ω2)1/2, α = – d –3[(4π)3V ′′′(r1) + (π4/b2)(ω2+4g)] < 0
d << d0
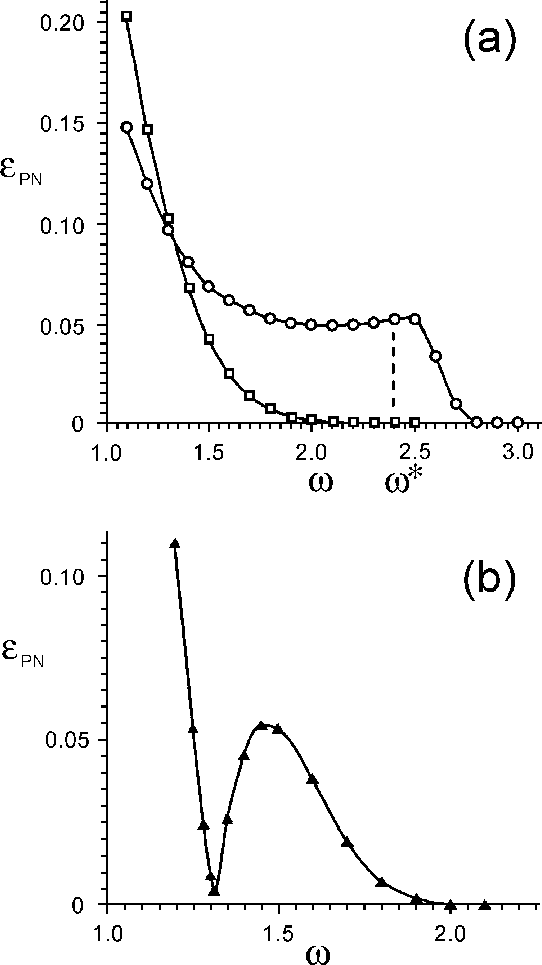
Simulation results for exponential interaction (θ=1, V0=200=fixed, ωy is varied):

conventional surface diffusion: D ≈ D0 exp[–(Esaddle–Em.e.)/kT]
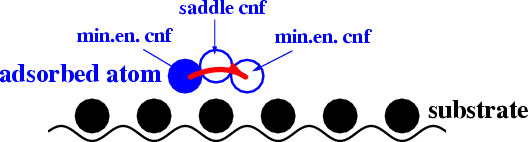
complicated exchange diffusion: D ≈ Dkink ρkink
where Dkink≈ kT /mkinkηkink and ρkink= C exp[–(Ekink–Em.e.)/kT]
![]()
![]()
![]()
The zigzag FK model was introduced by Braun and Kivshar (PRB 44 (1991) 7694) and then studied in details in the series of papers (pdf files may be found here):
| 2D substrate potential | 2D lattice of atoms |
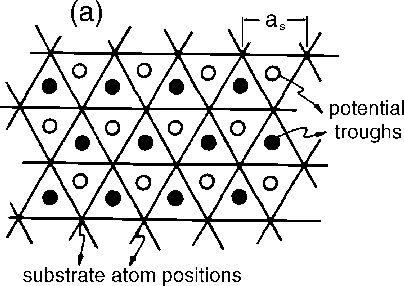 |
 |
Last updated on October 5, 2008 by Oleg Braun. Translated from LATEX by TTH