The Frenkel-Kontorova model: Introduction

The Frenkel-Kontorova (FK) model: Introduction

The FK model
Some applications
The ground state problem

The fixed-density chain: Aubry transition
The free-end chain: Devil’s staircase

Dynamics
Kinks
Hierarchy of kink lattices
Generalizations

The Frenkel-Kontorova model

Yakov Il'ich Frenkel & Tatyana Kontorova (1938)

Simplicity of the model:

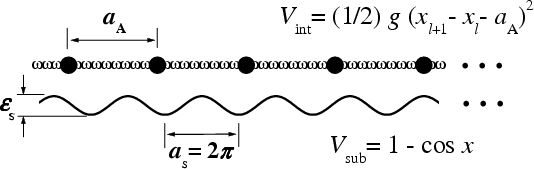
one-dimensional
classical mechanics
harmonic nearest-neighboring (NN) springs
sinusoidal substrate potential

System of units: m = 1, a = 2π, ε_s= 2

Parameters: (i) g (elastic constant) and (ii) a_A (lattice constant)

Limiting cases: g >> 1 or g ~ 1 or g << 1

Also important: a_A= 2π or a_A≠ 2π

Boundary conditions are also important. Variants:

free end(s) or

fixed density (in computer simulation – periodic b.c.)

Richness of the model

Mathematics

integrable equations (sine-Gordon equation → topological and dynamical solitons)
Østochastic theory (standard map: GS → Aubry (C/IC) transition; metastable excitations → glass-like behavior)

Physics – richness and complexity of the phenomena involved

nonlinear interaction laws
competing lengths → incommensurability effects
possible disorder due to pinning effects and intricacy of the excitation spectrum

Applications - everywhere where one may separate a subsystem, and treat the remainder as an external substrate potential, damping, and thermal bath; in particular:

dislocations; domain walls in ferroelectrics, ferro- and antiferro-magnetics
crowdions in solids; super-ionic conductors
proton transport in biological molecules and ice-like crystals
ladder of Josephson junctions
amorphous solids
submonolayers adsorbed on crystal surfaces (including such questions as phase diagram of the system, surface reconstruction, surface diffusion, crystal growth)
tribology

Some applications

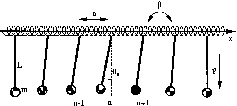
Mechanical model	Dislocation

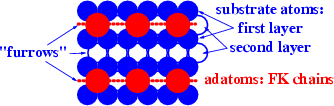
Adsorption on “furrowed” (metal) surfaces [fcc(110), bcc(112), hcp(1010)]	DNA

The ground state (GS) problem

I. The fixed density case (periodic boundary conditions)

Aubry transition: C (commensurate GS) → IC (incommensurate GS)

Potential energy: E(g,θ ) = ∑[V_sub(x_l) + V_int(x_l+1–x_l)] → min → g(x_l+1+ x_l–1– 2x_l) = sin x_l →

2D nonlinear area-preserving twist map (the Taylor-Chirikov standard map):

ì
í
î

x_l+1 = x_l + p_l+1

p_l+1 = p_l + g^–1 sin x_l

ü
ý
þ

Y_l+1 = TY_l where

Y_l Î (0,2p ) × (0,2p ) tour


enlarged view	enlarged view	enlarged view

orbits:

regular (points) or quasi-periodic (curves) g = ∞

g_c(w) ≈ 1 (for the golden mean w)

chaotic (stochastic) g = 0

( the most "survived" orbit corresponds to the golden mean w = (√5-1)/2 )

The GS of the FK model always corresponds to a regular orbit in the map
The GS is described by the hull function: x_l = h(la + β), where β is an arbitrary phase

For an irrational concentration, the Aubry transition by breaking of analyticity takes place:

for g > g_c(w) we have the sliding state [ h(x) is continuous], while

for g < g_c(w) we have the pinned state [ h(x) is discontinuous]

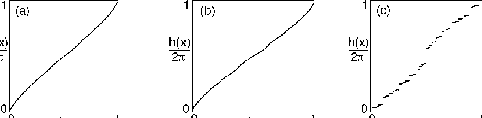
Note: metastable states correspond to glass-like configurations

II. The free-end chain: Devil’s staircase

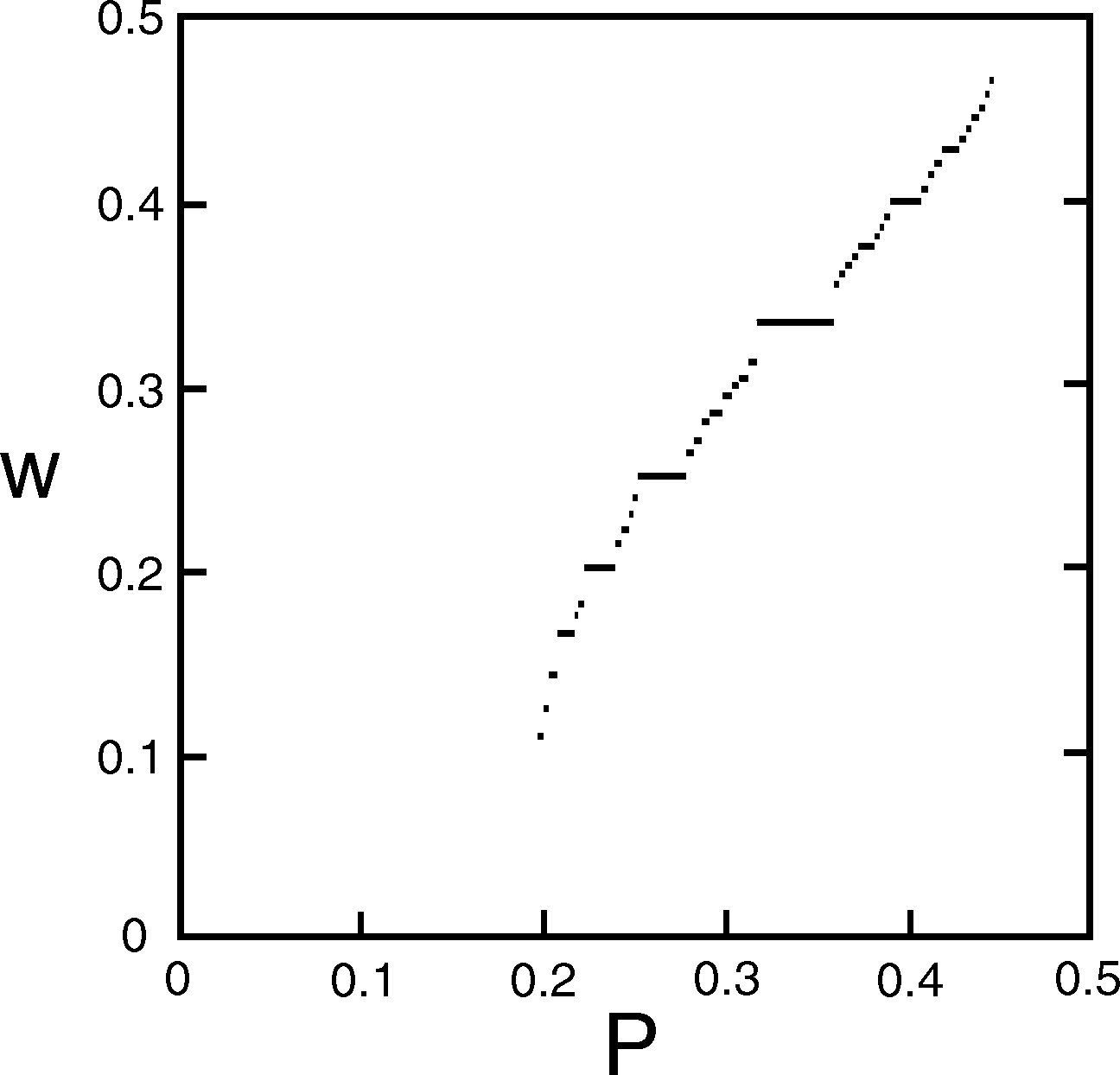
Frank – van der Merwe (FvdM) transition

Motion equation: d²x_l/dt² + sin x_l – g (x_l+1 + x_l–1 – 2x_l ) = 0
In the continuum-limit approximation we come to the sin-Gordon (SG) equation u_tt – u_xx+ sin u = 0
The SG equation is exactly integrable: any solution is a superposition of

phonons
breathers (dynamical solitons) u(x, t) = 4 tan^–¹{ [√(1– Ω²)/Ω] sin(Ωt) / cosh [x√(1–Ω²)] }
kinks (topological solitons) u(x, t) = 4 tan^–1 exp[ (x – vt)/√(1–v²) ]

Discreteness effects:

phonon spectrum: ω_ph(k) = [1 + 2g (1 – cos k)]^1/2, where |k| ≤ π
Peierls-Nabarro (PN) potential
metastable states
radiation of moving/oscillating solitons
localized (intrinsic, shape) kink modes

Kinks

antikink θ = 1 (trivial GS) kink is topologically stable minimally possible local extention (vacancy) or expansion (extra atom) of the commensurate GS structure
	min-en. cnf saddle cnf
Discreteness effects → PN potential ε_PN = E_saddle– E_min-en

θ = 3/5 (complex GS)
	kink GS antikink

Hierarchy of kink lattices

The original atomic FK lattice (example for θ = 4/3)

may be considered as a lattice of kinks constructed on the reference structure θ₀= 1. Indeed, let us consider kinks as quasiparticles of mass m_(kink) subjected to the periodic PN potential of the height ε_PN and interacting with the potential v_int(R) (R₀=3a_s). In such a way we come to

the renormalized FK model with the structure θ_(kink)= 1/3

is characterised by the elastic constant g_(kink)= a²v_int′′(R₀)/2π²ε_PN , and its excitations are superkinks / superantikinks

The case of θ = 1±δ, δ << 1:

GS = GS(θ=1) + residual (geometrical) kinks + thermally excited kink-antikink pairs

low temperature T (0 < k_BT < ε_superkink): residual kinks form a superlattice; excitations are superkinks

higher T (ε_superkink< k_BT < ε_{trivial
kink}): kink superlattice is “melted”; excitations correspond to the “trivial” (θ=1) kinks

Generalizations

substrate: nonsinusoidal such as PR (Peyrard-Remoissenet) or DSG (double sin-Gordon) potentials
interaction: anharmonic, long-ranged, nonconvex
2D FK models (phase diagrams, DW motion)
- 2D scalar FK model
- zig-zag model (transverse degree of freedom)
- 2D vector FK models (spring-and ball model; truly 2D model)
dc driven FK-type models (a nice applet for the dc driven FK model was written by F.-J. Elmer)
ac driven FK model

Next: Generalizations of the FK model

Back to main page

Last updated on October 5, 2008 by Oleg Braun