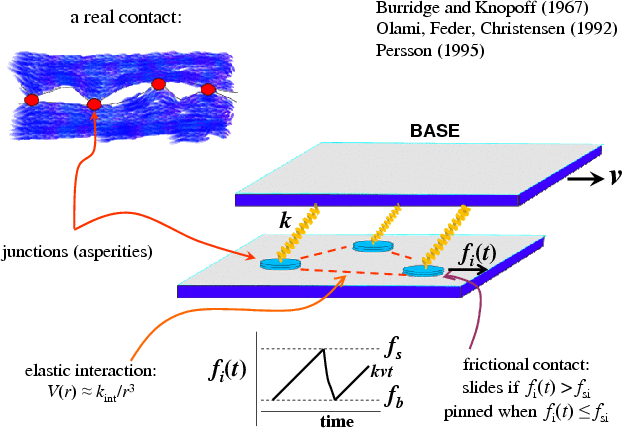
Transition from
Stick-slip to Smooth Sliding: An Earthquake-like Model
An earthquake-like model
presented below exhibits a “transition” from
stick-slip motion to smooth sliding at a velocity of the order of those
observed in experiments. The results show that experimentally observed
smooth sliding at the macroscopic scale must correspond to microscopic-scale
stick-slip motion (see also
 ).
).
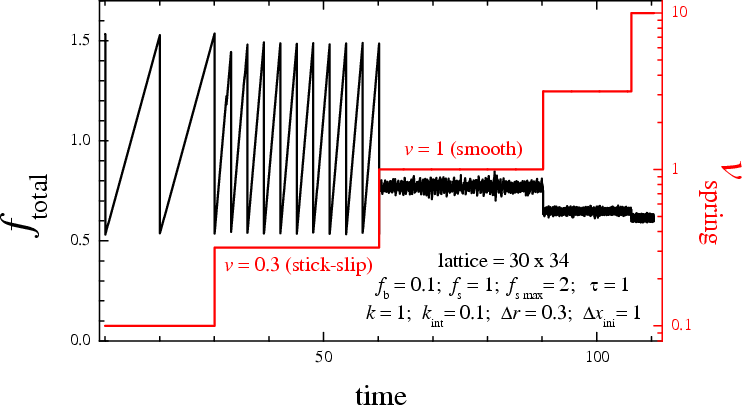
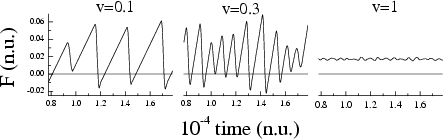
vc is the critical velocity of the transition from
stick-slip to smooth sliding.
Simulation (soft lubricant,
Vll=
1/9, Nl =
2, kspring=
3·10–4):
vc~
10–2c, or
vc~
1 to 10
m/s
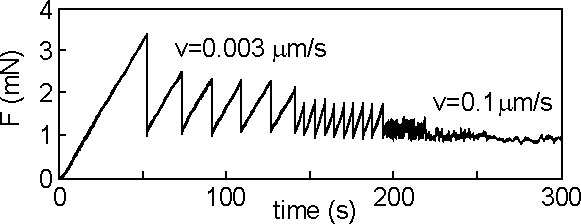
Experiment (friction force versus time at increasing sliding
velocity for grafted chain molecules; Ruina 1983, Israelashvili 1993;
from Persson’s survey 1999):
vc ~
0.1 to 1 μm/s
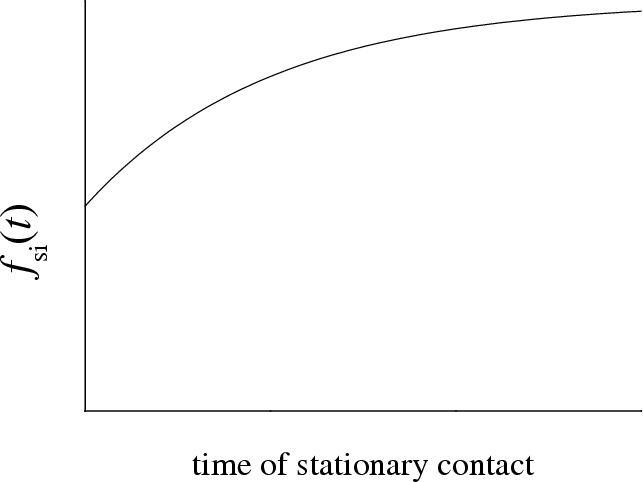
The main idea is to introduce in some way a macroscopic-scale characteristic
time τ (e.g., of order seconds) which will determine
the transition between two qualitatively different regimes, the regime of smooth
sliding and the regime of stick-slip motion. The most reasonable way is to
assume that the static frictional force depends on the time of stationary
contact, for example, let us assume that if the sliding-to-locked transition has
occur at t=0, then the static frictional force will evolve as
|
fs(t) = fs1
+ (fs2 – fs1)(1 – e–t/τ) . |
|
(Fs) |
One of possible mechanisms of a slow fs change with the time
of stationary contact (after the sliding-to-locked transition) is a plastic
deformation of a softer material, e.g., the lubricant. Possible mechanisms may
be
- the increase of the area of real contact with time
- squeezing out for simple (spherical) molecules [recall our
simulation result: fs(Nl)
~ exp(–...Nl)]
- inter-diffusion when the surfaces are covered by layers of
long-chain polymers (e.g. fatty acid monolayers)
Variants of the model:
(a) model: 1D
↔
2D
(b) lattice: regular
↔
random
(c) interaction: short-ranged
↔
long-ranged
(d) “stimulated” model
(when a junction relaxes, it
emits a wave burst
which stimulates other junctions to relax, too)
A minimal model:
to reproduce experimental dependencies,
(a) the model must be
2D
(b) the spatial distribution of junctions
must be random
(c) it must exist an interaction between the junctions (which
may be short-ranged)
(d)
the model must incorporate a dependence of the static frictional force
fs(t) on the time of stationary
contact, e.g., according to Eq.(Fs)
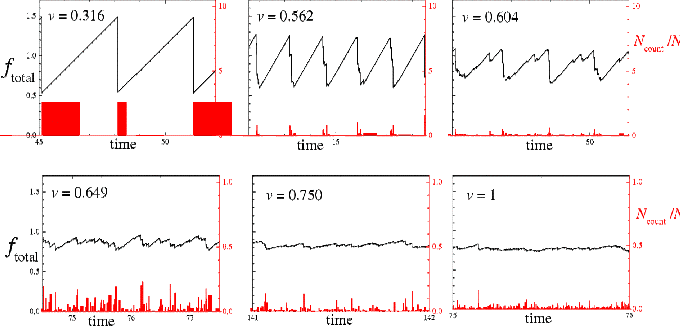
Here
Ncount /N
is a “size” of the avalanche. Note that the transition is smooth.
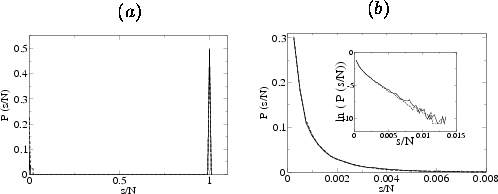
Figure: the distribution of avalanche
sizes P(s/N) at (a) v = 0.1 (solid curve) and
v = 0.2 (dotted curve), and (b) v = 3 (solid curve) and
v = 5 (dotted curve). The inset in (b) is a log-linear plot showing the exponential dependence.
Let us at time t a given (i-th) junction, pinned for an "age" τi, relaxes. Then the force on a neighboring (j-th) junction abruptly
increases by the amount Δfj
= [fsi(τi)
– fb]b, where b
= kij /(k + ∑j≠ikij′). For the triangular lattice with the parameters kij~
k we have ‹b›≈1/7.
The nearest neighboring junction, j, will relax too (and, thus, the
avalanche will start) if fj(t+0) = fj(t–0)
+ Δfj
≥
fsi(τj). In the high-velocity regime we can put fsi≈ fs, because ‹τi›
<< τ. The distribution of forces
P(fi) in this case
has a simple form (Persson 1995): it is constant for forces within the interval
fb< fi< fs
and zero outside it. Thus, the probability p that the j-th
junction will relax, i.e. that
fj(t–0)
≥ (1–b) fs,
is equal to p = b. Because there are six nearest neighbors
around the "starting" junction i, the probability to have an
avalanche of size s ≥ 2 is Ps(2) = 6p.
Then, the j-th junction may stimulate its own (five) nearest neighbors to
relax, thus the probability to have an avalanche of size s ≥ 3
is Ps(3) = Ps(2)×5p. Iterating, we have Ps(s) = νpPs(s–1),
or Ps(s) ~ (νp)s,
where 3 ≤ ν ≤ 5 [ν = 5 if the
avalanche forms a one-dimensional non-intersecting curve and
ν ≈ 3
when the avalanche is compact (2D)]. Using Ps(s) = ∫s∞ds′ P(s′),
we obtain for the avalanche distribution P(s)
~ exp(–s/s),
where the average size of the avalanche is
s = –1/ ln(νp). Thus, if static frictional force
does not depend on time, we always have νp < 1, so that s < ∞, so the avalanche cannot occupy the whole system. Taking
ν = 5 and p ≈ 1/7, we obtain
s ≈ 3 for the triangular lattice. This is in agreement with simulation which yields
s ≈ 4
for the v = 3 case. The fluctuations of the total frictional force scale as ‹f(t) –
‹f(t)»
~ N–1/2 ~ 1/√A
with the number of junctions N or the contact area
A. Note that similar considerations for the one-dimensional system
lead to ν=1 (the avalanche can expand in one
direction only) and p ≈ 1/3, so that
s ≈ 1.
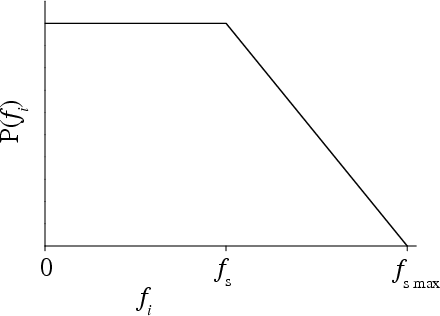
At a low velocity,
when the time dependence of the static frictional force is important, the
slipping of junctions becomes synchronized and an avalanche can occupy
the whole system. The distribution of forces P(fi) now has a more complicated form, it is constant for forces 0 < fi <
fs (here we put fb= 0 for
simplicity) and monotonically decreases to zero for forces fs<
fi< fsm. For purposes of an estimation let us assume that this decrease may be described
by a simple linear dependence,
P(fi) = 2(fsm– fi) / (fsm2– fs2) (see figure to the right). The condition that after the relaxation of the i-th junction, the nearest
neighboring junction j-th will relax too, now takes the form
fj(t–0)
≥ (1–b) fsi(τi).
The probability that the j-th junction will relax, is equal to
p = ∫f′fsm
df P (f) = ( fsm–
f′)2 / (fsm2– fs2),
where f′=‹(1–b) fsi(τi)›.
With the parameters used above, if we take ‹fsi(τi)› ≈ 0.5(fsm+
fs), we obtain p > 1/7. Moreover, if
‹fsi(τi)›
< 1.43, we obtain p > 1/5, so that νp > 1, and the avalanche will expand over the whole system.
-
The macroscopically observed “smooth” sliding corresponds to the atomic-scale
stick-slip motion (not resolved in experiment?).
-
The
macroscopic-scale stick-slip behavior emerges due to the concerted motion of the many junctions
because of their interaction.
-
The
transition itself is smooth.
-
The “transition” takes place at
vc~
a/τ, where a
is the average distance between junctions and
τ
is an “aging” time of a single junction.
Reasonable values for these
parameters (e.g., a ~10–6
to 10–3 m
and
τ
~ 1 to 103 s)
lead to experimentally observed values of vc
(see however
 )..
)..
Still open questions:
-
•nature of the junctions (asperities?
“solid islands”?)
-
mechanism of
the
fs(t) dependence
(squeezing out of the lubricant? aging of individual contacts? gradual increasing of the
contact area? coalescing of
contacts?)
See O.M. Braun and J. Röder, Phys. Rev. Lett.
88 (2002) 096102 "Transition from stick-slip to smooth sliding: An
earthquakelike model" (pdf files may be found
here)
NB: Thus, we came to the conclusion that in order to describe the
stick-slip to smooth sliding transition in agreement with experiments, the
system must (i) be 2D, (ii) include interaction between the
contacts, (iii) incorporate some chaos (in positions of contacts and in
the initial configuration), and (iv) include contact's aging. However,
above we used the model where all contacts are identical, while in a real
tribosystem, the contacts should be characterized by different parameters, e.g.,
different values for the static thresholds. In the next Chapter we show that the
model with a distribution of thresholds Pc(fs)
naturally describes meso- and macroscopic tribosystems. In such a model, the
items (i, ii) become not crucial, and the items (i, ii,
iii) just act to create the distribution of thresholds. As for aging, it
still is important to explain the dependence of system dynamics on the driving velocity vd.
Last updated on October 8, 2008 by Oleg Braun. Translated from
LATEX by
TTH
![]() ).
).